Ordinary Differential Equations and Linear Algebra
1 Definition and Examples
We will move on to the second order equation which arises
a lot in science and
engineering.
1.1 Definitions and First Example
Definition 1 A second- order differential equation
is an equation involving
the independent variable t and an unknown function y along with its first and
second derivatives. We will assume the second order derivative could be solved
explcitly. i.e. we will consider the equations of the form
y'' = f(t, y, y' )
A solution to the above equation is a twice continuously
differentiable function
such that
y'' (t) ≡ f(t, y(t), y' (t))
Example 1 Newton’s law of mechanics involves
acceleration, which is second
order derivative of the position function. i.e
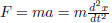The force may be
a function of the time t, the position x, and velocity dx/dt. So the second
order
ODE is
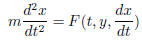
1.2 Linear Equation
We will focus on the Linear Equations . These
equation have the following
special form
y'' + p(t)y' + q(t)y = g(t)
(1)
As these are linear equations of y, y', y'' , we do not allow
1. the product of these to occur
2. nor any power higher than 1
3. nor any complicated function like sin y
to occur.
Similar to the case of first-order linear equation, we can
consider the homogeneous
equation associated with (1)
y'' + p(t)y' + q(t)y = 0
(2)
The homogeneous equation plays an important role in the
solution of second
order equations.
2 Existence and Uniqueness of Solutions:
You can always feel assured that if the coefficient p (t),
q(t), g(t) are good enough,
the solution to the initial value problem exists and is unique.
Theorem 1 (Existence and Uniqueness) Suppose the
functions p(t), q(t), g(t)
are continuous on the interval ( α, β ). Let t0 be any point in ( α, β ). Then
for
any real number
,
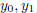there is one and only one function y(t) defined on ( α, β )
which is a solution to
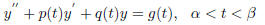
and satisfies the initial conditions
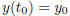and
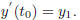
Remark:: The major difference of the theorem here
from the existence and
uniqueness theorem we talked about yesterday is you can be assured the solution
exists wherever p, q, g is defined and continuous. So this is a global theorem.
3 Structure of the general solution:
Proposition 1 Suppose that
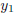and
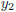are both solutions to the homogeneous,
linear equation
y'' + p(t)y' + q(t)y = 0
(3)
Then the function
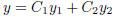is also a solution for any constants C1 and
C2. where we call y the linear combination of y1 and y2.
Example 2 For the simple harmonic motion equation
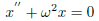
check x1(t) = cos
and x2 = sin
are both solutions to this equation. And so
is x(t) = C1x1(t) + C2x2(t).
It is easy to see x1(t) = sin
,
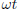x2(t) = cos
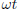are not constant multiples of
each other . Then we call them linearly independent.
Definition 2 Two functions u(t) and v(t) are said
to be linearly independent
on the interval ( α, β ) if neither is a constant multiple of each other over
that
interval. If one is a constant multiple of the other on ( α, β ), they are said
to be
linearly dependent there.
Example 3 check if the following pairs of functions
are linearly independent
or not.
1. x1 = sin t, x2 = sin t cos t
2. x1 = sin t, x2 = 0
3. x1 =
,
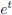x2 =
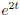
4. x1 = sin t, x2 = sin t
The aim of solving the second order linear ODE is to
express the solution
as a linear combination of 2 linearly independent solutions.
For example, two solutions are linear dependent on each other, namely
x1(t) = Cx2(t). Then C1x1(t) + C2x2(t) = (C1C + C2)x2(t) = C0x2(t).
Now the natural question to ask is how we can tell whether
2 functions are
linearly independent or not. Some of them are not very easy to judge at the
first glance.
We define the Wronskian of two functions u(t), v(t) to be
W(t) = u(t)v' (t) − v(t)u' (t)
he Wronskian could be used to tell if two solutions of the
linear homogeneous
second-order equation is linearly independent or not, due to the following
proposition:
Proposition 2 Suppose the function u and v are
solutions to the linear, homogeneous
equation
y'' + p(t)y' + q(t)y = 0
(4)
in the interval ( α, β ). Then u, v are linearly
independent if and only if the
Wronskian is identically zero .
Example 4 Exercise:
1. Compute the Wronskian of the solutions in example 2.
2. verify the solution of y'' +y' −6y = 0 is given by
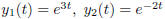
and y1, y2 are linearly independent.
3. verify the solution of y'' −2y' +2y = 0 is given by
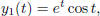y2(t) =
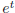sin t and y1, y2 are linearly independent.
| Prev | Next |