Polynomials
Definitions. A polynomial in m variables is a function
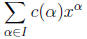
where I is a finite subset of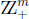 
of
multi-indices 
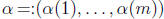, and the corresponding
monomials are defined by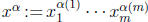 
. Polynomials are
treated as formal expressions
in algebra and as functions on IRm or Cm in analysis. The (nonzero) numbers c(α )
are called
coefficients of p . The index α of the monomial occuring in p that is highest in a
chosen
monomial order determines the degree of p. In the univariate case, the degree is
just the
biggest power of the variable that occurs in p. In the multivariate setting,
various orders are
possible, so the same polynomial may have different degrees depending on the
order chosen.
Univariate polynomials are by now well understood.
Fundamental theorem of algebra . Every nonzero univariate polynomial p of degree
n
with complex coefficients has exactly n roots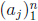 
in C and can be factored as
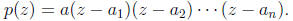
Uniqueness theorem. If p and q are univariate polynomials of degree at most n
and
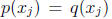for j = 1, 2 ...,m where
are distinct complex
numbers and
m > n, then p and q are identical.
Theorem [ division algorithm ]. If f and g are univariate polynomials and g is not
the
zero polynomial , then there exist unique polynomials q and r such that
f(x) = q(x)g(x) + r(x)
where either r is the zero polynomial or deg r < deg g. The quotient q and the
remainder r
can be found by synthetic division .
Bezout's theorem. The remainder from the division of a polynomial f(x) by x-a
is equal
to f(a).
Theorem [univariate polynomial interpolation]. For any sequence
of complex
numbers and a set of n distinct points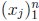 
from C, there exists a unique polynomial p of
degree at most n - 1 such that
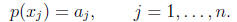
Examples.
1. Find the remainder when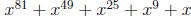 
is divided by
.
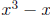2. Let p be a nonconstant polynomial with integral coefficients . If n(p) is the
number of
distinct integers k such that (p(k))2 = 1, prove that n(p) - deg(p) ≤ 2 where deg(p)
denotes the degree of the polynomial p.
3. Factor (a + b + c)3 - (a3 + b3 + c3).
4. Find a if a and b are integers such that x2 - x - 1 is a factor of
.
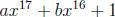5. Let r ≠ 0 be given. Find the polynomial p of degree at most n that satisfies
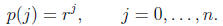
6. Find the unique polynomial p of degree n that satisfies
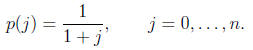
Hint: consider (x + 1)p(x) - 1.
7. A polynomial p of degree 990 satisfies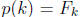 
for k = 992, 993,
...,
1982, where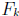 
denotes the kth Fibonacci number. Prove that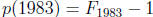 
.
| Prev | Next |