Polynomials in One Variable and Factoring
An expression of the form
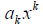
where k is a whole number and
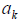is a constant, is
called a monomial. A sum of monomials forms a
polynomial where each monomial is called a term.
Polynomial in Standard Form:
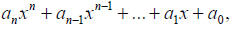
where
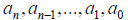are coefficients, and n ≥ 0 is an
integer.
If
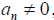then
n – degree,
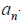– leading coefficient,
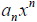– leading term.
Polynomial? Yes/No Coefficients Degree
Adding and Subtracting Polynomials
Polynomials are added and subtracted by combining
like terms . The like terms are the monomials which
may differ only by the coefficients.
Example. Perform the indicated operation .
(3x4 + 2x3 − x) − (−x4 + x2 + x −1) =
Two polynomials are multiplied by using Properties of
Real Numbers and Laws of Exponents .
Example: (4x5 ) ∙ (3x2 ) =
Example: Find the product.
(2x4 − 3x2 +1)(4x3 − x) =
Use FOIL when multiplying two binomials .
(FOIL – First, Outer, Inner, Last)
( y − 3)(2y + 5) =
Special Products and Factoring
(x − y)(x + y) =
Squares of Binomials, or Perfect Squares :
(x + y)2 =
(x − y)2 =
Cubes of Binomials, or Perfect Cubes:
(x + y)3 =
(x − y)3 =
Difference of Two Cubes:
(x − y)(x2 + xy + y2 ) =
Sum of Two Cubes:
(x + y)(x2 − xy + y2 ) =
Factoring is a process of finding polynomials whose
product is equal to a given polynomial.
Example: Expand or factor by using the special product
formulas :
(a) (x + 3)(3− x) =
64x2 − 81=
(b) (7x + 5)2 =
4x2 + 28x + 49 =
(c) (2 − x)(4 + 2x + x2 ) =
8c3 + 27 =
(d) (2x − 3)3 =
Factoring out the Common Factor :
The CF of a polynomial is formed as a product of the
factors (numbers, variables , and/or expressions)
common to all terms, each raised to the smallest power
that appears on that factor in the polynomial.
Remember when factoring out the CF, we use the
Distributive property
ab + ac = a(b + c)
that is, we divide each term by the CF.
Example:
8x5 y3 + 6xy9 =
5x2 (x − 2)3 + x(x − 2)2 =
Factoring by Grouping
This method is used when the terms can be collected in
two or more groups such that there is a common factor
in all groups.
Example: Factor by grouping.
2x3 − 5x2 − 8x + 20 =
Prime (Irreducible) Polynomials
A polynomial is called prime or irreducible over a
specified set of numbers if it cannot be written as a
product of two other polynomials whose coefficients
are from the specified set.
A polynomial is considered to be factored completely
over the particular set of numbers if it is written as a
product of prime over that set polynomials.
Example: Determine which of the polynomials below
is/are prime over the real numbers
x2 + 9
y2 −10
Factoring a Second-Degree Trinomial
FOIL “in reverse” can be used for factoring the
trinomials over the integers.
(ax + b)(cx + d ) = ac ∙ x2 + (ad + bc) ∙ x + bd
Example: Factor the trinomials.
2x2 + 5x − 3 =
6x2 −17x +12 =
Factoring by substitution
Example: 16(x +1)2 + 8(x +1) +1=
Example: Factor completely over the integers by any
method .
(x −1)3 − 64 =
x6 + 7x3 − 8 =
5(3 − 4x)2 − 8(3 − 4x)(5x −1) =
b6 − 27 =
x6 − y6 =
| Prev | Next |