Review of Linear Equations

Math D. 1.4

We begin with a review of linear equations .

Definition 0.1 A linear equation in one variable x is an equation that can
be written in the form

ax + b = 0,

where a and b are real numbers , and a ≠ 0.

Solving a linear equation means finding all values of x for which the equation
is true.

For example 4 is a solution to the equation 3x = 12 because 3(4) = 12. We
call the set of solutions the solution set.
Two equations are equivalent if they have the same solution set.

Property 0.1 Addition and Multiplication Properties of Equality

•The Addition Property of Equality
The same real number or algebraic expression may be added to both
sides of an equation without changing the equation 's solution set.
a = b and a + c = b + c are equivalent equations .
•The Multiplication Property of Equality
The same nonzero real number may multiply both sides of an equation
without changing the equation's solution set.
a = b and ac = bc are equivalent equations when c ≠ 0.

Example 0.1 Using Addition and Multiplication Properties of Equality

•x - 5 = 12 Add 5 to both sides
x - 5 + 5 = 12 + 5
x = 17

•x + 5 = 12 Subtract 5 from both sides
x + 5 - 5 = 12 - 5
x = 7

•4x = 24 Divide both sides by 4
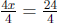so after simplification x = 6

•x/3 = 5 Multiply both sides by 3
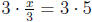so after simplification x = 15

Example 0.2 Solving a linear equation
3x + 8 = 50 First we take care of addition/subtraction
3x + 8 - 8 = 50 - 8 so 3x = 42 Now divide both sides by 3
x = 14

Property 0.2 Solving Linear Equations
1. Simplify the algebraic expression on each side.
2. Collect all variable terms on one side and constant terms on the other.
3. Isolate the variable and solve
4. Check your solution by substituting the proposed value for x

Example 0.3 Solving Linear Equations
5x - (2x - 8) = 35
5x - 2x + 8 = 35
5x - 2x = 27
3x = 27
x = 9
Check.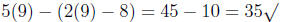

Example 0.4 Solving Linear Equations
5y - 2 = 9y + 2
5y - 4 = 9y
-4 = 4y
y = -1
Check.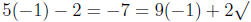

If a linear equation involves fractions , it is easiest to eliminate the fractions
and then solve the remaining equations as above.

Example 0.5 Linear Equation involving Fractions

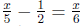
The LCD of 5, 2, 6 is 30

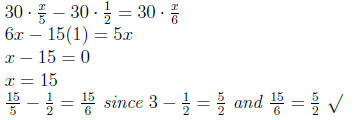
Example 0.6 Linear Equation involving Fractions

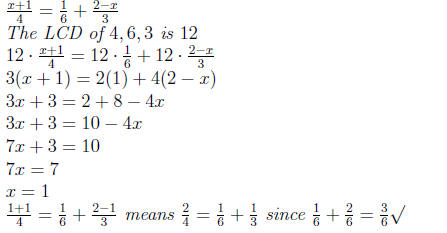
Definition 0.2 Types of Equations

•An equation that is true for all real numbers is called an identity.
x + 5 = x + 2 + 3

•An equation that is not an identity, but is true for at least one real number,
 is called a conditional equation. These are the types of equations
we have been working with so far.
x = 5

•An inconsistent equation is an equation that is not true for a single real
number.
x = x + 3 this solution set is written as the empty set ,

Example 0.7 Types of Equations
•4x + 7 = 7(x + 1) - 3x
4x + 7 = 7x + 7 - 3x
4x + 7 = 4x + 7 is an identity

•4(y + 5) = 21 + 4y
4y + 20 = 4y + 21 in inconsistent
,

Example 0.8 Application Problems
The formula N = .12x + .4 models the number of motorcycles sold in the
United States, N, in millions, x years after 1998. When will motorcycle
sales reach 2.2 million?
N = .12x + .4

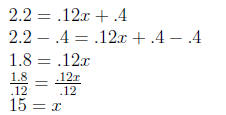
So fifteen years after 1998, 2013, motorcycle sales will reach 2.2 million