Solutions to Odd-Numbered Exercises and Practice Tests
1. Find the value of the other five
trigonometric functions , given
tan x = 4/11,sec x < 0.
2. Simplify
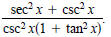
3. Rewrite as a single logarithm and simplify
ln| tanθ |-ln| cotθ |.
4. True or false: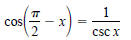
5. Factor and simplify : sin4x + (sin2x)cos2x
6. Multiply and simplify : (cscx + 1)(cscx - 1)
7. Rationalize the denominator and simplify: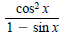
8. Verify: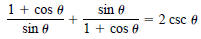
9. Verify: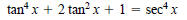
10. Use the sum or difference formulas to determine :

11. Simplify:

12. Verify
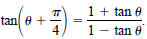
13. Write
sin(arcsinx - arccosx) as an
algebraic expression in x .
14. Use the double-angle formulas to determine :

15. Use the half-angle formulas to determine:

16. Given sin = 4/5,θ lies in Quadrant II, find cos(θ/2).
17. Use the power - reducing identities to write
(sin2x)cos2x
in terms of the first power
of cosine.
18. Rewrite as a sum : 6(sin 5θ)cos2θ.
19. Rewrite as a product :
sin(x + π) + sin(x - π).
20. Verify
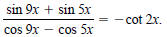
21. Verify: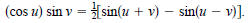
22. Find all solutions in the interval
4sin2x = 1
23. Find all solutions in the interval
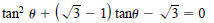
24. Find all solutions in the interval
sin2x = cosx
25. Use the quadratic formula to find all solutions in the interval
tan2x - 6tanx + 4 = 0
| Prev | Next |