Solving Equations I-Expressions Involving Power Functions

Applying the Toolbox—Solving Equations

Example 2.5 Solve the equation -3x(x +1) = -(x +1) ( x² + 2).

Guess and plug in method . The following table gives the outcome of plugging in
various numbers into the left -hand and right-hand sides of this equation.

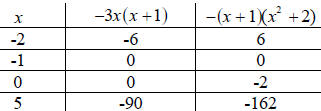
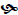Here the value of the left-hand side
equals the right-hand side.

So far, we’ve identified that when x = -1, the left-hand side of the equation equals the right-hand
side. Are there any other values of x which do the same? How do you know? This is
a very poor method.

Graphing method to estimate solutions. Instead of guessing which numbers to plug in, we
could graph y = -3x(x +1) and y = -(x + 1) ( x² + 2) on the same set of axes to get a more
complete picture. Finding the values of x which solve the equation is the same as finding
the x- coordinates of the points where the graphs of y = -3x(x +1) and y = -(x + 1)  ( x²+ 2)
intersect (or cross).

Use your graphing calculator to graph y = -3x(x +1) and y = -(x + 1)  ( x²+ 2) on the same
axes. Change your viewing rectangle to make sure you are seeing all the important features
of your graphs. Trace and zoom to estimate the x-coordinates of the points where the two
graphs cross. Are any of your answers close to x = -1? Are there any other solutions?

Questions to ponder over the semester: How do you know that you have found all the
solutions? Is your viewing rectangle large enough? These questions are not so easy to
answer, but you will be able to by the end of the semester.

Using a graphing calculator will only allow you to estimate the solutions. We need to use
algebra to find exact solutions. But using both graphing and algebra in the exercises will
increase your understanding and allow you to check your answers.

Algebraic method. We’ll use our toolbox in a series of steps.

Preliminary work. Get all terms which are on the right-hand side of the equation over to
the left by adding or subtracting them to each side. With all your mental powers, resist
the temptation to cancel out anything by dividing. You will only miss possible solutions.
Here we add (x +1)( x²+ 2) to each side to get

-3x(x +1) + (x + 1)(x² + 2) = 0.

Combine all like terms. Deconstruct the left-hand side—play with it! How do you know
when you have what you need? Experience and practice! Our end goal is to turn the left
side into a product of expressions and then use the Zero Law .

One way to deconstruct the left part of the left-hand side is to see it as a product of
x +1and -3x . The right part is the product of x +1 and x² + 2. We have identified a
common factor of x +1:

	identify the common term,
	factor it out.

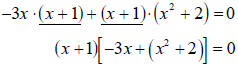Now at this stage we pause and check: are there any other common terms in the leftover
pieces? There are no other common terms but if there were, we would factor them out in
the same way. Continue the process of identifying common terms and factoring them
out, until there are no more. Then add or subtract the leftovers. Our equation now looks
like

(x +1)( x²- 3x + 2) = 0.

This quadratic term can be factored (always check for this), so we end up with

(x +1)(x - 2)(x -1) = 0.

Use the Zero Law. We did this part of the problem in Example 2.4. The Zero Law says
that the solutions of (x +1)(x - 2)(x -1) = 0 are the same as the solutions of x +1 = 0,
x - 2 = 0, and x -1 = 0. Thus our final answers are x = -1, 1, 2.

How do these solutions compare to the answers you estimated with your graphing
calculator?

Example 2.6 Solve the equation

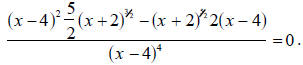
Graphing Method. Following the previous example we see that we want to graph the
left-hand side and the right-hand side on the same set of axes. We can estimate the
solutions to this equation by tracing and zooming in on the points of intersection. Try
this in this case. Remember that y = 0 is just the x-axis. What happens near x = 4 ? In
fact, your calculator is confused—it has no idea what to do at x = 4 .

Using our brains, we see that plugging in x = 4 gives a zero denominator. This means
that the left-hand side of the equation is undefined at x = 4 .

We can graph the left-hand side with our graphing calculators as long as we have the
calculator avoid x = 4 . To do this, we must graph the function in two pieces—first with
x values smaller than 4, and then with x values larger than 4.

Step 1: Graph y = 0 and

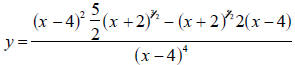
on the same set of axes using a viewing window with a maximum x-coordinate of 3.5 or
3.99 (or anything just a bit smaller than 4).

Step 2: Graph these same functions using a window with a minimum x-coordinate of
4.01 or 4.1 (or something just a bit larger than 4).

In each step trace and zoom to estimate the x-coordinates of any place where

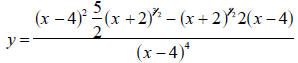
crosses the x-axis (which happens to be the second function y = 0 ).

Algebraic Method. Here we already have everything but zero on the left-hand side.
Since the left-hand side contains algebraic fractions , we want to multiply through (both
sides of the equation) by the common denominator to get rid of the algebraic fractions.
In this case the common denominator is (x - 4)⁴ . We now want to solve this revised
equation.

Any x-value which is a solution of the original equation will be a solution to this revised
equation. This means that we will find the solutions to the original equation among those
to the revised equation

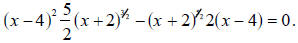
Read that last sentence carefully—a very important fact is that in solving the revised
equation, we may get x-values which are not solutions to the original equation. So we
have a two-step process: solve the revised equation, then check to see which of these
values are really solutions to the original equation. This last step is called checking for
extraneous solutions.
Solve revised equation. Solve the equation

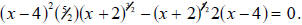
This is one complicated algebraic expression subtracted from another. When your
equation is of this form, combining like terms will often help simplify it . We will follow
the form of the examples in the Toolbox.

First notice that there is a factor of both x - 4 and x + 2 in each side of the minus
symbol. We will take the smallest power of each of these terms as our common term.
The smallest power of x - 4 is 1 and the smallest power of x + 2 is 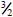. With the
common terms underlined, our equation looks like

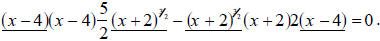
We now factor out the common terms and subtract the leftovers in the following series of
steps.

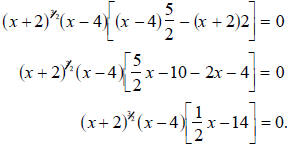
At this point the left-hand side of the equation is now the product of three simpler
equations. Use the Zero Law! The solutions to this equation are the solutions to the three
equations

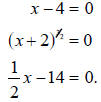
The first and third are linear equations yielding the solutions x = 4 and x = 28
respectively. The middle equation can be solved by raising each side to the power ,
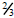which is the reciprocal of the power . Thus its solution is x = -2

Remember our two-step process! These x-values may be the solutions to the revised
equation, but they may not even be in the domain of the left-hand side function. We have
to worry about zeros in the denominator as well as negative numbers under a square root ,
fourth root, etc.

Checking for extraneous solutions. The easiest way to do this is to just start plugging in
to the original equation the (possibly false) solutions that you have already obtained.
When you plug in an x-value, do you really get zero on the left? Or must you conclude
the left-hand side is undefined at that x-value? We see that if we plug in x = -2 and
x = 28 to the original equation we really do get 0 = 0 . But we have already seen that
x = 4 gives a zero denominator. So our solutions to the original equation are only
x = -2,28. How do these check out with the solutions you estimated with the graphing
method?

Preliminary work. Get all terms to the left-hand side of the equation, leaving only zero
on the right-hand side. Convert all negative exponents into positive exponents. If you
have algebraic fractions, multiply through by the common denominator, and continue to
the next step to solve this revised equation.

Tips on solving equations without algebraic fractions. It generally helps to keep
asking yourself the following series of questions in order over and over again. If you
answer yes to any of them, follow the instructions.

Q1. Basic Questions: Is the left-hand side of the equation a linear, quadratic, or other
polynomial that can be factored? If yes, …you know what to do. Is the entire left-hand
side raised to a power? If yes, raise each side to the reciprocal of that power to
get rid of it, and then repeat question Q1.

Q2. Is the left-hand side of the equation a product of algebraic expressions? If yes, use
the Zero Law to break the original equation into smaller equations. Repeat the
question process (starting with Q1) to solve each smaller equation.

Q3. Are there any like terms? If yes, combine them following the examples in the
toolbox. Go back to Q2.

If these steps do not lead to a complete solution, you should try anything else you can
think of. But you might have to rely on the numerical estimates you obtained from
graphing (or some other source).

Check for extraneous solutions. Plug in to the original equation all solutions obtained
above. Do you get zero in the denominator? Or a negative number under a square root,
fourth root, etc? Later on in the course, we will see other ways extraneous solutions will
occur. Any solution which gives any kind of problem like this is NOT really a solution.
All other solutions are your answers. Check them against the graphing estimates.