Techniques of Integration
1 Integration Tools
In many ways, the operation of differentiation can be condensed into a black
box: once all the rules are known , one can simply create an algorithm to
analyze any expression and apply those rules as necessary to obtain the
desired result. In most cases, no creativity or ingenuity is needed to perform
differentiation. However, integration is quite the opposite. Every integral is
different and requires a different combination of techniques and methods to
derive the answer. In essence, integration is an art.
In all that follows, we shall omit including the constant of integration when
giving expressions for the antiderivatives, but the reader should always be
mindful of its implied presence.
1.1 The Basics
For completeness, we shall include the basic integration formulas including
the inverse power rule , and some basic trigonometric integrals .
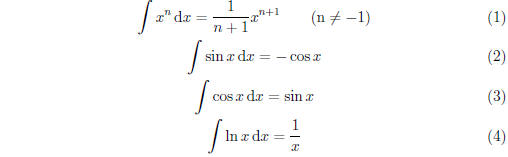
1.2 u-Substitution
The method of u- substitution is a change of variables in an attempt to transform
the integrand to something that is recognizably integrable. It is here
where we first see that integration requires some adroitness. The method of
u-substitution can be summarized as follows :
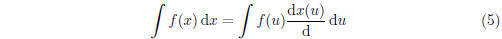
1. Select of function of x (normally a portion of the
integrand) to mold
into a new variable u. I.e. make a definition of a new variable u in
terms of x . This requires some foresight in that we hope to also find
u'(x) in the integrand so that we can complete u-substitution. (see step
4.)
2. Calculate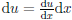 
3. Replace the expression u(x) in the integrand with the variable u wherever
appropriate.
4. Identify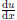 
in the integrand and replace
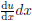with du. This is often
the stumbling point in u-substitution.
Hopefully, at the end of these steps, we end up with an integral that we
know how to compute. Just as a picture is worth a thousand words, so much
more valuable an example is than the theory:
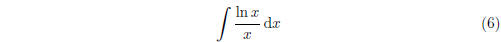
In order to compute this integral, we notice that it is
not an integral of
any basic form and so we do not have any rules that we can immediately
apply to determine the answer. However, after staring at the page for a
minute or two, we may finally realize that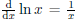 
so
if we define u(x)
to be ln x, then u'(x) is in the integrand and we can complete the steps in
u -substitution. Putting it all down on paper we have:
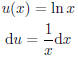
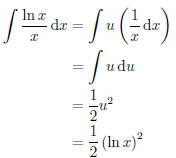
1.3 Properties and Identities of Mathematical Functions
There are many situations in which very nasty-looking integrals actually have
relatively simple solutions because the integrand can be greatly simplified by
using identities of functions. For example,
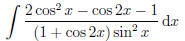
may look like a relatively complicated integral at first
glance. However,
by using some trigonometric identities, we can see that in fact the integrand
reduces to 1, and so this integral is trivially easy to compute. While the
above example may be an extreme case of simplification, many seemingly
untractable problems become quite manageable after some applications of
such identities. Below are a few examples of identities and properties to keep
in mind while trying to integrate expressions.
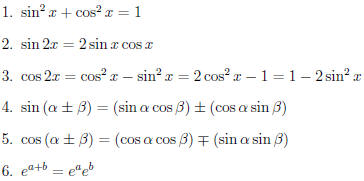
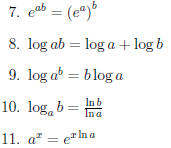
1.4 Integration by Parts
There are some integrals that cannot be dealt with by any of the means
dictated so far. Actually, there are many such integrals. A very powerful
tool is the integration by parts formula. The one dimensional case can be
derived from the product rule :
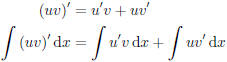
Rearranging terms, we obtain
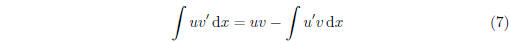
The power of this method can be seen in the following way:
suppose we
are trying to integrate a product of two functions, where one function is the
derivative of something (e.g. v'). Then using this method, we essentially
transfer the derivative onto the other function u and supplement such an action
with a correction term, uv. This operation of ”transferring derivatives”
is indeed very useful in integrating a great many things. In order to illustrate
the idea, we consider an example.
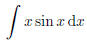
No previous techniques are applicable to this example.
However, let us
consider using integration by parts. We want to ”transfer” a derivative from
one term onto another. We notice that f(x) = x is the derivative of
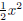and
that g(x) = sin x is the derivative of −cos x. If we transfer a derivative from
f(x) to g(x), we will end up trying to integrate something proportional to
x 2 cos x, which is hardly better than we started off with. However,
if instead
we do the opposite, we will only have to integrate cos x, which is quite within
our capabilities. We then proceed as follows:
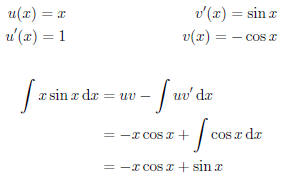
1.5 Trigonometric Substitution
When doing u-substitution, we were looking to assign a more complicated
function of x a very compact name (namely u). In this form of substitution,
we want to expand the variable x from itself into a trigonometric function.
The motivation for this is as follows: suppose we wanted to integrate something
like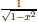 
. None of the tricks we have learned so
far enable us to do
this. But what if the x2 in the denominator were a sin2 u
instead? Then
we could use our trigonometric identity 1 − sin2 x = cos2
x to get rid of the
square root sign and integrate the result. We now present the mathematics
of this substitution:
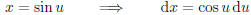
Then our integral transforms as follows
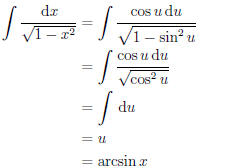
A trigonometric substitution allows us to deal with terms
of the form
a−bx2, bx2 −a, and a+bx2 which are under a
square root. The idea is that
we wish to coalesce the two terms into one and then get rid of the square
root. In certain cases we are even able to use trigonometric substitution to
deal with higher powers of x that may be raised to a fractional power other
than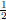 
.
| Prev | Next |