The Major Topics of School Algebra
Quadratic Equations
Before approaching quadratic equations, students need some firm grounding in the
concept of a square root, which is more subtle than usually realized. Given a
positive
number s , then there is one and only one positive number r so that r2
= s. The fact
that there is such an r is not trivial to prove, and, in fact, cannot be proved
in school
mathematics. But the fact that there is at most one such r, i.e., the
uniqueness of this
r, can be demonstrated with care to eighth graders and beyond. By definition,
this r
is called the square root of s, and is denoted by
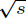 . Thus by the definition of the
. Thus by the definition of the
notation, 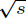 is always ≥ 0. From the
uniqueness of the square root, one concludes the
is always ≥ 0. From the
uniqueness of the square root, one concludes the
critical fact that
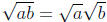 for all positive a, b
for all positive a, b
This fact is usually either left unexplained, or relegated
to verification by calculator for a
few special cases. We recommend that it be carefully explained (proved), not
only because
students can learn from such reasoning, but also that they need to learn such
reasoning
to prepare them for advanced mathematics.
Now let x be a number. Then a quadratic equation in one variable is an
equality of
the form (or can be brought to this form by the associative, commutative, and
distributive
laws) ax2 +bx+c = 0 which asks for all the real numbers x that make this
equality valid
(a, b, c are constants and a ≠ 0). A solution, or a root, of the equation is a
real number
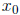 which satisfies the equation, i.e.,
which satisfies the equation, i.e., 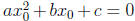 . To
solve the equation is to find
. To
solve the equation is to find
all the solutions of the equation. It may be pointed out to students at the
outset that,
unlike the case of a linear equation in one variable, some quadratic equations
do not have
solutions, e.g., x2 + 3 = 0.
The method of solution dates back to the Babylonians some four thousand years
ago.
It consists of two steps:
(A) One can solve all quadratic equations of the form a(x + p)2 + q = 0, if it
has a solution.
(B) All quadratic equations can be brought to the form in (A) by the use of
the associative, commutative, and distributive laws .
Solving (A) is relatively straightforward: if it has a solution, it has to be
one of two
possibilities:

Again, the precise method of arriving at these solutions is worth repeating.
First, if
we assume that there is a solution 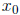 , then we have an equality among numbers:
, then we have an equality among numbers:
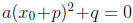 , from which we conclude that
, from which we conclude that 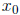 must have one of the two possible
values
must have one of the two possible
values
as above. This does not say that these values are indeed solutions of a(x + p)2
+ q = 0.
For that, we have to directly verify that
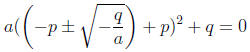
This is a routine computation. The point, however, is that solving a quadratic
equation
involves nothing but computation with fixed numbers. The consideration of
“variables”
does not enter.
A little reflection is in order at this point. For
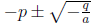 to be solutions (i.e., points
to be solutions (i.e., points
on the number line), necessarily q/a ≤ 0, because there is no square root of a
negative
number in the sense defined above. Conversely, as we have seen, if we know q/a <
0, then
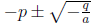 are solutions. Thus we have proved, incidentally, that
are solutions. Thus we have proved, incidentally, that
a(x + p)2 + q = 0 has solutions
 q/a ≤ 0.
q/a ≤ 0.
The proof of (B) of course depends on the technique of completing the square. On
the one hand, this step is decisive for the solution, and is not one that yields
easily to
discovery learning. On the other hand, once the idea of completing the square is
accepted,
its implementation is quite routine. Indeed, if we know in advance that ax2 + bx
+ c can
be brought to the form a(x+p)2 +q for some suitable p and q, then expanding the
latter
by the distributive law gives
ax2 + bx + c = ax2 + 2apx + (ap2 + q)
Comparing the coefficients of both sides, we conclude that letting
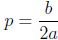 and
and 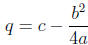
should work. Indeed it does, as a simple computation shows. Another way, equally
valid,
of looking at this process is to ask what can be put in the box to make the
expression
within the parentheses a square:
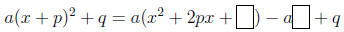
Bearing in mind that (x2 + 2kx + k2) = (x + k)2, we easily come to the same
answer.
Recalling the earlier formula for the roots of a(x + p)2 + q = 0 as
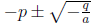 , we have
, we have
now obtained the famous quadratic formula for the roots of ax2 + bx + c = 0:
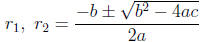
(Note that this derivation requires the use of the identity
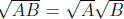 .) The earlier
.) The earlier
reasoning about the solvability of a(x + p)2 + q = 0 leads to a similar
conclusion:
ax2 + bx + c = 0 has solutions
![]() b2 − 4ac ≥ 0.
b2 − 4ac ≥ 0.
Completing the square is a basic technique in school mathematics, and its
significance
goes beyond getting the roots of a quadratic equation. When we get to the
discussion of
quadratic functions, for example, we will see how it leads to a complete
understanding of
their graphs.
It remains to bring closure to this discussion by mentioning that, if the
quadratic
polynomial ax 2 + bx + c (a ≠ 0) already comes in the form
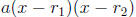 for
some
for
some
numbers 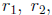 then solving the quadratic equation
then solving the quadratic equation
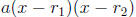 becomes
becomes
extremely pleasant: the roots are 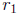 and
and
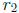 . This is because the following basic
fact about
. This is because the following basic
fact about
numbers implies that 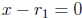 or
or
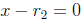 .
.
If pq = 0 for two numbers p and q, then one of p and q is
0.
The proof of this fact should be emphasized in the classroom: By FASM, we may
act as
if p and q are both rational numbers , which may be taken to be quotients of
integers. So
suppose p ≠ 0, we will prove that q = 0. Indeed, multiply both sides of pq = 0
by the
reciprocal 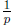 of p, we get immediately q = 0, as desired.
of p, we get immediately q = 0, as desired.
The long and short of it is that, if a quadratic polynomial is already factored
as a
product of linear polynomials , then the corresponding quadratic equation can be
solved
by inspection. This is certainly one reason why the factoring of quadratic
polynomials
is of interest, and this fact can be used to motivate the usual exercises on
factoring such
polynomials.
It is a remarkable fact that, conversely, if we can solve a quadratic equation,
then we
also obtain a factorization of the corresponding quadratic polynomial. Let
ax2+bx+c = 0
be given. Denoting the roots given by the quadratic formula by 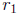 and
and 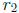 as
above, then
as
above, then
we claim that the following identity in x is valid:
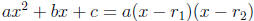 for all x
for all x
Why this is remarkable is that it allows us to recover the whole expression ax 2
+ bx + c
completely as the product of 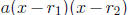 as soon as we get to know the two
values of
as soon as we get to know the two
values of
x at which ax2 +bx+c becomes 0 (i.e.,
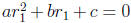 and
and 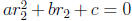 ). This can
). This can
be explained as follows. From the explicit expression of the roots
![]() of
ax2+bx+c = 0
of
ax2+bx+c = 0
in terms of a, b, and c (i.e., the quadratic formula), we obtain the following
interesting
relations between the roots and the coefficients of a quadratic polynomial:
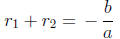 and
and 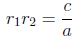
Therefore,
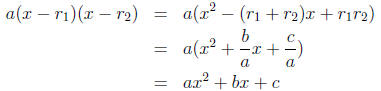
which is the asserted identity.
In particular, we see that factoring quadratic polynomials can be made entirely
mechanical:
just use the quadratic formula to get the roots and apply the preceding
identity.
Students should be made aware of this perspective to the factoring of quadratic
polynomials.
Many students do not see that the identity
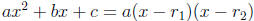 requires
requires
any proof. This is an example of a not-uncommon confusion between a simple
statement
(if 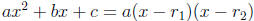 for all x, then
for all x, then 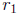 and
and 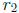 are the roots)
and its not-so-
are the roots)
and its not-so-
simple converse (if 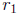 and
and 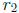 are the roots, then
are the roots, then 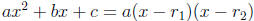 for
for
all x). From this instance, we can see the need to stress reasoning in school
mathematics.
If the quadratic polynomial is x2 + bx + c, i.e., if a = 1, then the preceding
relations
between the roots and the coefficients simplify to
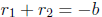 and
and 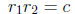
These attractive relations between roots and coefficients have generalizations
to polynomials
of any degree.
The ability to solve quadratic equations greatly enlarges the range of word
problems,
which up to this point involve only linear phenomena. One particular example is
the
problem of finding the rectangle having the greatest area among all rectangles
with a
fixed perimeter.
| Prev | Next |