TOURNAMENT OF THE TOWNS

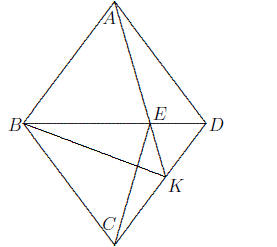
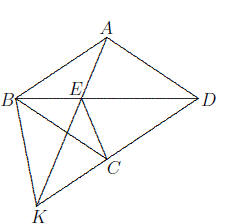
1. Let ABCD be a rhombus. Let K be a point on the line CD , other than C or D, such that
AD = BK. Let P be the point of intersection of BD with the perpendicular bisector of BC.
Prove that A, K and P are collinear.

2. (a) Each of Peter and Basil thinks of three positive integers . For each pair of his numbers,
Peter writes down the greatest common divisor of the two numbers . For each pair of
his numbers, Basil writes down the least common multiple of the two numbers . If both
Peter and Basil write down the same three numbers, prove that these three numbers are
equal to each other.
(b) Can the analogous result be proved if each of Peter and Basil thinks of four positive
integers instead?

3. Michael is at the centre of a circle of radius 100 metres. Each minute, he will announce the
direction in which he will be moving. Catherine can leave it as is, or change it to the opposite
direction. Then Michael moves exactly 1 metre in the direction determined by Catherine.
Does Michael have a strategy which guarantees that he can get out of the circle, even though
Catherine will try to stop him?

4. Two players take turns entering a symbol in an empty cell of a 1 × n chessboard, where n
is an integer greater than 1. Aaron always enters the symbol X and Betty always enters the
symbol O. Two identical symbols may not occupy adjacent cells. A player without a move
loses the game. If Aaron goes first, which player has a winning strategy?

5. Attached to each of a number of objects is a tag which states the correct mass of the object.
The tags have fallen off and have been replaced on the objects at random. We wish to
determine if by chance all tags are in fact correct. We may use exactly once a horizontal lever
which is supported at its middle. The objects can be hung from the lever at any point on
either side of the support. The lever either stays horizontal or tilts to one side. Is this task
always possible?

6. The audience arranges n coins in a row. The sequence of heads and tails is chosen arbitrarily.
The audience also chooses a number between 1 and n inclusive. Then the assistant turns one
of the coins over, and the magician is brought in to examine the resulting sequence. By an
agreement with the assistant beforehand, the magician tries to determine the number chosen
by the audience.

(a) Prove that if this is possible for some n, then it is also possible for 2n.
(b) Determine all n for which this is possible.

7. For each letter in the English alphabet, William assigns an English word which contains
that letter. His first document consists only of the word assigned to the letter A. In each
subsequent document, he replaces each letter of the preceding document by its assigned word.
The fortieth document begins with “Till whatsoever star that guides my moving.” Prove that
this sentence reappears later in this document.

Note: The problems are worth 5, 3+3, 6, 7, 8, 4+5 and 9 points respectively.

Solution to Junior A-Level Fall 2007

1. Let AK intersect BD at E. We shall prove that BE = CE, so that E lies on the perpendicular
bisector of BC. It will then follow that E = P, and that A, P and K are indeed collinear.
Since AD = BK and AB is parallel to DK, ABKD is a cyclic quadrilateral. It follows
that ∠AKD = ∠ABD = ∠CBD, so that BCKE is also a cyclic quadrilateral. We now have
∠ECB = ∠EKB = ∠ADB = ∠EBC, so that EB = EC.

2. (a) First Solution by Jarno Sun:
Let the numbers Peter thinks of be p₁, p₂ and p₃, the numbers Basil thinks of be
b₁, b₂ and b₃, and the numbers both write down be w₁,w₂ and w₃. Note that each
of gcd(w₁,w₂), gcd(w₂,w₃) and gcd(w₃,w₁) is equal to gcd(p₁, p₂, p₃). Similarly, each
of lcm (w₁,w₂), lcm(w₂,w₃) and lcm(w₃,w₁) is equal to lcm(b₁, b₂, b₃). It follows that
w₁w₂ = gcd(w₁,w₂)lcm(w₁,w₂) = gcd(w₂,w₃) lcm(w₂,w₃) = w₂w₃, so that w₁ = w₃.
Similarly, w₂ shares this common value.

Second Solution:
Let the numbers Peter thinks of be x, y and z. We assume to the contrary that
gcd(x, y), gcd(x, z) and gcd(y, z) are not the same number. Then there must be a prime
p such that the highest powers of p which divide these three numbers are not identical.
Let the highest powers of p which divide x, y and z be a, b and c respectively. We may
assume that a ≤ b ≤ c. Then the highest powers of p which divide gcd(x, y), gcd(x, z)
and gcd(y, z) will respectively be a, a and b, and we have a < b. Now the highest power
of p which divides any of Basil’s numbers must be b, and 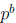will divide two of his least
common multiples . It follows that the two sets of three numbers cannot be identical
unless all three numbers in each set are the same.

(b) The answer is no. Peter’s numbers may be 1, 2, 2 and 2. Then his six greatest common
divisors are 1, 1, 1, 2, 2 and 2. Basil’s numbers may be 1, 1, 1 and 2. Then his six least
common multiples are 1, 1, 1, 2, 2 and 2. The two sets of numbers are identical, but the
six numbers in each set are not all the same.

3. Michael can escape. In the first move, he chooses any direction. Catherine cannot gain
anything by reversing it. In each subsequent move, Michael chooses a direction which is
perpendicular to the line joining his current position to the centre of circle. Again Catherine
cannot gain anything by reversing it. Let 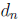be the distance of Michael from the centre of the
circle after the n-th move. We have d₁ = 1 and 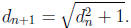We claim that 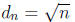for
all n ≥ 1. The basis holds, and by the induction hypothesis, 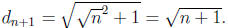It
follows that after 10000 moves, Michael will arrive at the circumference of the circle.

4. We claim that Betty can guarantee a win. We first prove the following auxiliary result.
Suppose the first cell is marked X and the last cell is marked O, with n vacant cells in
between. If Aaron goes first, he loses. We use induction on n. When n = 1, neither player
has a move. Since Aaron moves first, he loses. Assume that result holds up to n−1 for some
n ≥ 2. Consider a board with n vacant cells between the X and O already marked. In his first
move, Aaron will partition the board into two, with i and j vacant cells respectively, where
i + j = n − 1. In the first board, the first and the last cells are marked X. Betty places an O
next to either X. Then we have two boards each of which has X at one end and O at the other,
with less than n vacant cells in between. Aaron will lose because by the induction hypothesis,
he loses on both boards. We now return to the vacant 1 × n board. Suppose Aaron marks
an X on the k-th cell. By symmetry, we may assume that k > 1. Betty marks an O on the
first cell. It is Aaron’s move, and by the auxiliary result, he will lose if k = n−1 or n. If not,
he will at some point be forced to mark an X on the 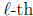cell where 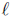≥ k + 2. Then Betty
will mark an O on the (k + 1)st cell, and the auxiliary result applies again. Thus Aaron is
forced to open up new parts of the board again and again. Eventually he runs out of room
and loses. It follows that Betty can always win if n ≥ 2.

5. Solution by Dmitri Dziabenko.
Let there be n objects, and let the mass indicated by the tag on the i-th object be m_i,
1 ≤ i ≤ n. We may assume that m₁ ≤ m₂ … ≤ m_n. Arbitrarily choose positive numbers
d₂ < d₃ < · · · < d_n and choose d1 so that d₁m₁ = d₂m₂ + d₃m₃ + · · · + d_nm_n. On one side of
the support, hang the 1-st object at a distance d1 from the support. On the other side of the
support, hang the i-th object at a distance di from the support for 2 ≤ i ≤ n. Let the correct
mass of the i-th object be ai for 1≤ i ≤ n. We consider three cases.

Case 1. All the tags are in fact correct.
Then we will have equilibrium.

Case 2. The tag on the 1-st object is correct but those on some of the others are not.
Then {a₂, a₃, . . . ,a_n} is a permutation of {m₂,m₃, . . . ,m_n}, and by the Rearrangement Inequality,

d₂a₂ + d₃a₃ + · · · + d_na_n < d₂m₂ + d₃m₃ + · · · + d_nm_n = d₁m₁.

Case 3. The tag on the 1-st object is incorrect.
Then m₁ < a₁ = m_j for some j, 2 ≤ j ≤ n. Hence d₁a₁ = d₁m_j > d₁m₁ while

d₂m₂ + d₃m₃ + · · · + d_nm_n
> d₂m₁ + d₃m₂ + · · · + 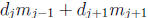+ · · · + d_nm_n
≥ d₂a₂ + d₃a₃ + · · · + d_na_n,

and again we have no equilibrium.

6. (a) Given a row of n coins arbitrarily arranged heads and tails, and a number between 1 and
n inclusive, the assistant can flip exactly one coin so that the magician can tell which
number has been chosen. With a row of 2n coins and a number m between 1 and 2n, the
magician and the assistant place the numbers 1 to n in order in the first row of a 2 × n
array, and the numbers from n+1 to 2n in order in the second row. If the row number
h and the column number k of the location of m are determined, then m = (h−1)n+k.
The magician and the assistant also consider the 2n coins as in a 2×n array. Code each
coin with heads up as 0 and each coin with tails up as 1. Compute the sum of the codes
of the two coins in each column modulo 2 and regard the result as a linear array of n
coded coins. By the hypothesis, the assistant can flip the q-th coded coin to signal the
number k to the magician. This can be achieved by flipping either of the two coins in
the q-th column. To signal the number h to the magician, the assistant will just use the
bottom coin of the q-th column, code 0 meaning h = 1 and code 1 meaning h = 2. If the
bottom coin is not correct, flip it. Otherwise, flip the top coin.

(b) For n = 1, the assistant must flip the only coin. However, the chosen number can only
be 1, and the magician does not require any assistance. Hence the task is possible. For
n = 2, let the coins be coded as in (a). The assistant will just use the second coin, code
0 meaning h = 1 and code 1 meaning h = 2. If the second coin is not correct, flip it.
Otherwise, flip the first coin. Hence the task is also possible. By (a), the task is possible
whenever n is a power of 2. We now show that the converse also holds. Each of the 2ⁿ
arrangement of the coins codes a specific number between 1 and n. If n is not a power of
2, then 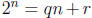where q and r are the quotient and the remainder obtained from the
Division Algorithm, with r > 0. By the Pigeonhole Principle, some number is coded by
at most q arrangements. Each may be obtained by the flip of a single coin from exactly
n other arrangements. The yields a total count of qn < 2ⁿ. On the other hand, from
each of the 2ⁿ arrangements, we must be able to obtain one of these q arrangements by
the flip of a single coin. This contradiction shows that the task is impossible unless n is
a power of 2.

7. Solution by Central Jury.
Let the i-th document be D_i, 0 ≤ i ≤ 40. Note that D₀ consists only of the letter A, and
D₁ consists only of the word assigned to the letter A. This word does not start with A, as
otherwise all documents start with A, which is not the case since D₄₀ starts with T. However,
the word assigned to A does contain the letter A, so that D₁ contains D₀, and not from the
beginning. Similarly, 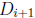contains D_i for 0 ≤ i ≤ 39, again not from the beginning. Note
that no D_i can start with a single-letter word, as otherwise this word will start all subsequent
documents, which is not the case since D₄₀ does not start with a single-letter word. Since
there are only twenty-six letters in the English alphabet, D_j and D_k must start with the same
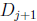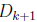letter for some j and k where j < k ≤ 27. Then and start with the same word,
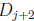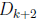and start with the same two words, and so on. Let t = 40−k. Since k ≤ 27, t ≥ 13
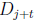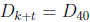so that and start with the same thirteen words, including “Till whatsoever
star that guides my moving”. Since D₄₀ contains a copy of 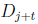and not from the beginning,
this sentence will reappear in D₄₀.