Algebra Quiz 3 Solutions
1. Let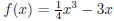 
. Find the
critical numbers for f , and identify the open intervals on which
it is increasing or decreasing.
To find the critical numbers, we find f'(x) and set it to zero; then we solve
for x :
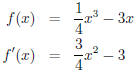
(now we set it to zero...)
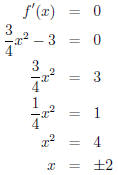
These critical numbers split the real line into three
intervals: (−∞,−2), (−2, 2), and (2,∞). On
each interval, we must decide whether the function increases or decreases— or
equivalently , whether
its derivative is positive or negative. We pick numbers, one from each interval:
say, -3, 0, 5. We
evaluate f'(x) at each of these numbers:
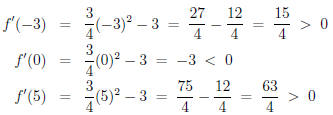
Of course, we don’t really care about the specific
numbers; all we want to know about is the sign!
Since f'(−3) > 0, this means that f(x) increases on the interval containing -3,
which is to say
(−∞,−2). Since f'(0) < 0, we conclude that f'(x) < 0 throughout the interval
(−2, 2); on that
interval, f decreases. Finally, f increases on the interval (2,∞) because f'(5)
> 0.
That answers the question, but I’d like to show you a way to solve the problem
with less raw
computation. (Because, no calculators on tests !)
With the derivative written as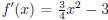 
, you have to
go pretty much all the way through
with your computation in order to know whether f'(c) is positive or negative,
for whatever c you
have in mind. But if you rewrite it, things get better:
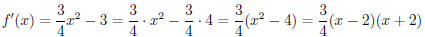
Using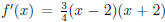 
, we can evaluate
the sign of f '(c) without getting all numerical.
Watch:
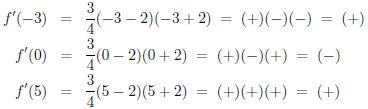
...where “(−)” just means “some negative number ” and “(+)”
means “some positive number”. Some
of you learned this method (or a variant) in high school. As long as you use a
valid method, I don’t
particularly care which method you use. Anyway, these results repeat the ones we
got above, and
we could now write down the same final answers. The key to this “signs only”
approach is to write
the funtion (in this case, the function f') in multiplicative form —that is,
write it as a product or
quotient of factors. Our derivative was originally in additive form; it was a
sum or (more accurately)
difference of terms . Additive form is great when you want to take a derivative.
Multiplicative form
is often better when you want to know whether the object is positive or
negative. Being comfortable
switching between the two will make you a stronger math nerd. Hoo-ah!
2. Find the absolute extrema of g(x) = 4x3 − 3x2 − 6x on
the interval [-1,2]. (State which is
max/min)
Absolute extrema can occur at critical numbers and at endpoints. The endpoints
are given, so let’s
find ourselves some critical numbers. We take the derivative:
g'(x) = 12x2 − 6x − 6 = 6(2x2 − x − 1) = 6(2x + 1)(x − 1).
Any x value that makes this zero or undefined is a critical number—but in this
case, it’ s a polynomial
(defined everywhere), so we just look for zeroes. If 2x + 1 = 0, then
If x − 1 = 0, then
. We have our contestants: the endpoints -1
and 2, and the critical numbers 
and 1. The
question is: who has the most extreme y- coordinate ? Let’s plug them in and find
out.
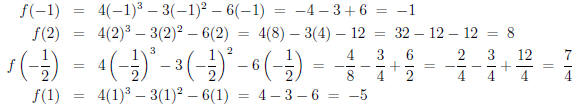
We see that the absolute maximum, 8, occurs at x = 2,
while the absolute minimum, -5, occurs at
x = 1. A sufficient answer would be: Abs Max=8 and Abs Min=-5.
I think there was one big pitfall on this problem, and that was in finding the
roots of g '. I factored
it, but if factoring isn ’t your bag, you might have tried the quadratic formula.
If that’s your
approach, make life easy for yourself by getting rid of the 6 first! Check it
out: we want to solve
12x2 − 6x − 6 = 0.
12x2 − 6x − 6 = 0←Divide by 6
2x2 − x − 1 = 0 ←Apply
Quadratic Formula
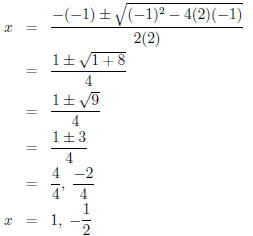
Contrast that lovely progression with the mess that
results if we just apply the quadratic formula
at the beginning (affectionately called the brute force method):
12x2 − 6x − 6 = 0 ← Apply Quadratic
Formula
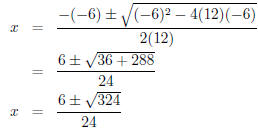
Most people would look at
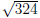and throw up their hands in defeat. This
approach can be
salvaged. . . but the right simplification at the right time can save you so
much anguish.
| Prev | Next |