math 108 Study Objectives

MATH 108 is built around the objectives listed in the Syllabus and Calendar, and each
exam question specifically addresses one of them. In stating an objective, we have certain
skills and knowledge in mind. The statements are concise, however, and so might not
convey those things to students as clearly as we would like. The discussions below are an
attempt to remedy that. We outline the skills and concepts that constitute an objective,
describe the kinds of questions that a student should be able to answer, and give a few
examples. The discussion is not a substitute for the explanations and examples in the text
and software; rather, it is a summary that a student might read after working with those
materials, perhaps when preparing for a quiz or exam.

Unit 1. Linear Equations and Inequalities

Objective 1a. Solve formulas, and use formulas to solve applied problems.

Text section and exercises
1.4, Evaluating and Solving Formulas, #1–55

Software lesson
1.4b, Evaluating Formulas

A formula is an equation that describes a general relation between two or more quantities.
For example, the formula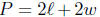 relates the perimeter P of a rectangle to the length
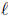and width

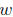
Typical questions. You should be able to solve a given formula for a specified variable—
that is, rewrite the formula so that one side consists of the variable by itself and the other
does not involve that variable. Given numerical values for all but one of the variables, you
should also be able to determine the value of the remaining variable.

Example. Solve the formula for w.
Solution: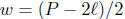

Example. Use the formula to find the width of a rectangle whose
perimeter is 42 inches and whose length is 12 inches.
Solution: 9 inches

Objective 1b. Solve absolute-value equations and inequalities, and express the
solution in algebraic , set or interval, and graphical notation.

Text sections and exercises
1.3, First Degree Equations and Absolute Value Equations, #61–80
1.6, Linear Inequalities and Absolute Value Inequalities, #55–75

Software lessons
1.3c, Solving Absolute Value Equations
1.6b, Solving Absolute Value Inequalities

Recommended software lesson for review
1.6a, Solving Linear Inequalities

The objective here is to solve equations and inequalities such as |x + 2| = 5 or |x − 1| ≤3
that involve absolute values. Absolute value equations can have two solutions, and absolute
value inequalities can have infinitely many solutions; in fact, the solutions of an absolute
value inequality typically constitute one or more intervals in the real number line . To solve
the equation or inequality means to describe the set of solutions, and there are three ways
to do that: algebraically reduce the inequality to specific conditions such as x = −7, x = 3
or −2≤ x ≤4; use set or interval notation such as {−7, 3} or [−2, 4]; or graph the solution
set on the real number line. Sometimes the solution set is the entire real number line, and
sometimes the equation or inequality has no solutions.

Typical questions. Given an absolute-value equation or inequality, you should be able to
describe the solution set algebraically, in set or interval notation, and graphically.

Example. Solve |x − 3| = 10 algebraically. Then give the solution set using set
notation, and graph it.
Solution: x = −7 or x = 13; {−7, 13}; graph omitted

Example. Solve |x + 2| > 5 algebraically. Then give the solution set using interval
notation, and graph it.
Solution: x < −7 or x > 3; (−∞,−7) ∪(3,∞); graph omitted

Objective 1c. Determine the slope and intercepts of the line defined by a linear
equation in standard, slope-intercept, or point-slope form, and graph the line.

Text sections and exercises
2.2, Slope-Intercept Form: y = mx + b, #13–41, 55–59
2.3, Point-Slope Form y − y₁ = m(x − x₁), #16–23, 48–53
Software lessons

2.2, Graphing Linear Equations in Slope-Intercept Form
2.3a, Graphing Linear Equations in Point-Slope Form

The objective here is to obtain information about a line, such as its slope and intercepts,
from an equation for the line and use that information to graph it. The equation might
be given in standard form Ax + By = C, slope-intercept form y = mx + b, or point-slope
form y − y₁ = m(x − x₁). An equation of the form y = c describes a horizontal line, and
one of the form x = c describes a vertical line. Parallel lines have the same slope, and the
slopes of perpendicular lines are negative reciprocals of each other .

Typical questions. You should be able to tell when a given a linear equation describes a
horizontal or vertical line. More generally, given a linear equation in any form, you should
be able to determine the slope of the line that the equation describes and determine the
x- and y-intercepts. Finally, you should be able to determine whether the lines described
by two given equations are parallel, perpendicular, or neither by computing their slopes.

Example. Determine the slope and intercepts of the line y = 3x − 6, and graph it.
Solution: Slope 3; y-intercept −6; x-intercept 2; graph omitted

Example. Determine the slope and intercepts of the line x = 3, and graph it.
Solution: Undefined slope (a vertical line); no y-intercept; x-intercept 3; graph omitted

Example. Determine whether the lines 2x + y = 4 and y = 3x + 1 are parallel,
perpendicular, or neither.
Solution: Slopes are −2 and 3, respectively, so neither parallel nor perpendicular.

Objective 1d. Compute the slope of a line given two points on the line, and
find any form of the equation of a line given two points on the line or slope
information and one point.

Text sections and exercises
2.2, Slope-Intercept Form: y = mx + b, #1–12, 42–49
2.3, Point-Slope Form y − y₁ = m(x − x₁), #1–15, 24–36

Software lessons
2.3a, Graphing Linear Equations in Point-Slope Form
2.3b, Finding the Equation of a Line

This objective is the reverse of Objective 1c; it is to obtain an equation for a line given
information that determines the line.

Typical questions. You should be able to rewrite a given equation for a line in another
form, such as slope-intercept form. In other questions that ask for an equation of a line, at
least one point on the line will be given. (Note: To know an intercept is to know a point.)
The key to obtaining an equation is then to find the slope. That might be given, or you
might need to compute it from other information, such as a second point that is on the line
or a statement that the line is parallel or perpendicular to some other given line. Having
the slope, you can immediately write down a point-slope equation y −y₁ = m(x−x₁) and
rearrange if necessary to obtain slope-intercept or standard form.

Example. Find the slope-intercept equation of the line 2x − 5y = 7.
Solution: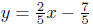

Example. Find the slope of the line through (1, 2) and (4,−5).
Solution: −7/3

Example. Find a standard-form equation for the line through (3,−1) with slope 1/2.
Solution: x − 2y = 5 (other solutions possible)

Example. Find an equation for the horizontal line through (−2, 5).
Solution: y = 5

Example. Find a point-slope equation for the line through (1, 3) that is perpendicular
to the line y = 5x − 2.
Solution: y − 3 = −1/5 (x − 1)

Unit 2. Systems of Linear Equations and Their Applications

Objective 2a. Graph linear inequalities in two variables.

Text section and exercises
2.5, Graphing Linear Inequalities, #1–30

Software section
2.5, Graphing Linear Inequalities

A solution of an inequality in two variables is a pair (x, y) for which the inequality holds.
For example, (1, 0) is a solution of 2x − 3y < 5, but (7, 2) is not. The solutions of a
linear inequality constitute a half-plane—one of the two sides of the line determined by
the corresponding linear equation. One can graph the solution set as a shaded region by
first sketching the line that the equation describes, using a dashed line if the inequality is
> or < to indicate that the solution set does not include the line, and using a solid line if
the inequality is ≥or ≤ to indicate that the solution set includes the line. One can then
choose any point not on the line and insert it into the inequality; if the point is a solution,
then the solution set is the half-plane containing it, and if not then the solution set is the
other half-plane.

Typical questions. Be able to choose the solution set of a given linear inequality in two
variables from among several graphs.

Objective 2b. Use graphing to determine whether a system of two linear
equations in two variables is consistent, inconsistent, or dependent.

Text section and exercises
3.1, Systems of Linear Equations (Two Variables), #1–10

Software lesson
3.1a, Solving Systems of Linear Equations by Graphing

Unit 2 concerns systems of two equations such as {2x+y = 5, x−3y = −2}. A solution is a
pair (x, y) that satisfies both equations. One can understand such a system by graphing the
two linear equations on a common set of axes. Each graph is a line, and the solutions of the
system are the points (x, y) that the lines have in common. There are three possibilities:

1) The lines cross. In this case, the system has exactly one solution—the intersection
point (x, y). Such a system is said to be consistent.
2) The lines are parallel. In this case, the system has no solution. Such a system is said
to be inconsistent.
3) The lines are the same. In this case, the system has infinitely many solutions—namely,
all the points on the line. Such a system is said to be dependent.

Typical questions. Given a linear system, and given the graph of the two equations involved,
you should be able to say how many solutions the system has—one, none, or
infinitely many—and whether the system is consistent, inconsistent, or dependent.

Objective 2c. Solve a system of two linear equations in two variables using
graphing, substitution, and addition.

Text section and exercises
3.1, Systems of Linear Equations (Two Variables), #1–36

Software lessons
3.1a, Solving Systems of Linear Equations by Graphing
3.1b, Solving Systems of Linear Equations by Substitution
3.1c, Solving Systems of Linear Equations by Addition

Graphing a consistent system yields two intersecting lines, and one can solve the system, at
least approximately, by reading the coordinates of the point (x, y) where the lines intersect.
Two other methods, called substitution and addition, allow one to solve the system exactly.
In both, the first step is to obtain a single equation involving just one of the two variables—
say, x—and solve that equation. The second step is to “back-substitute” the resulting value
of x in either of the two original equations to get an equation involving only y and then
solve that equation. If, in attempting to solve for y, one obtains a false equation such as
3 = 0, then the system is inconsistent. If one obtains an equation that is always true, such
as 3 = 3, then the system is dependent.

Typical questions. Given a consistent system and the graphs of the two equations involved,
you should be able to read off the solution (x, y). In other problems, given a system but
no graphs, you should be able to determine whether the system is consistent, inconsistent,
or dependent. If it is consistent, you should also be able to determine the value of x or y
using either substitution or addition (your choice). Finally, you should be able to perform
back-substitution; that is, given a linear system, and given the value of one of the variables,
you should be able to determine the value of the other variable.

Example. How many ordered pairs solve the system {2x − y = 5, −4x + 2y = 0}? Is
this system consistent, inconsistent, or dependent?
Solution: None; inconsistent

Example. The following system has a unique solution: {x + 2y = 3, 2x − 5y = 1}.
Use any method to find the x-coordinate of the solution.
Solution: 17/9

Example. The following system has a unique solution: {3x − 4y = 71, 3x + 2y = 5}.
The x-coordinate of the solution is 9. Find the y-coordinate of the solution.
Solution: −11

Objective 2d. Use systems of two linear equations in two variables to solve
applied problems, including mixture, interest, and motion problems.

Text section and exercises
3.2, Applications, #1–35

Software lesson
3.2, Applications (Systems of Equations)

In applications, one often knows two pieces of information about two quantities and can
represent that information by a linear system. Solving the system, one can then determine
both quantities. Objective 2c addresses all the steps in this process: setting up the linear
system, solving it, and interpreting the mathematical solution as it applies to the original
problem. The hardest step is to set up the system. The key is to recognize and give variable
names to the two unknown quantities; those might be amounts of the two ingredients in a
mixture, amounts of money invested at two different interest rates, or speeds in a problem
concerning motion. Rereading the problem with those two variables in mind, one sees that
the given information constitutes two linear equations involving the variables.

Typical questions. Each exam question addresses either just one part of the process (setting
up a linear system in an applied problem or using a system that is already set up to
determine one or both of the quantities in the problem) or it addresses the entire process.

Example. Dolly invests $15,000 in two different accounts, one paying an annual interest
rate of 5% and the other paying 7%. After one year, she receives a total of $930
interest. Let x be the amount invested at 5% and y the amount invested at 7%. Set
up, but do not solve, a system of equations that can be used to determine the amount
invested at each rate.

Solution: {x + y = 15000, (.05)x + (.07)y = 930}

Example. A chemist mixes a solution that is 15% alcohol with one that is 32% alcohol
to produce 20 liters of a mixture that is 25% alcohol. If x is the number of liters of 15%
solution and y the number of liters of 32% solution, then this problem is described
by the system of equations {x + y = 20, (.15)x + (.32)y = 5}. Determine the number
of liters of 15% solution needed for this mixture. Round your answer to the nearest
tenth of a liter.

Solution: 8.2 liters

Example. A private jet flies the same distance in 6 hours that a commercial jet flies in
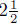hours. The speed of the commercial jet is 75 mph less than three times the speed
of the private jet. Given that the commercial jet’s speed is 300 mph, find the speed
of the private jet.

Solution: 125 mph

Unit 3. Polynomial and Rational Equations

Objective 3a. Use methods such as finding the greatest common factor, grouping,
perfect squares, difference of squares , and sum and difference of cubes to
factor trinomials and other polynomials completely.

Text sections and exercises
4.4, Introduction to Factoring, #1–60
4.5, Special Factoring Techniques, #1–58

Software lessons
4.4b, Special Factorizations—Squares
4.4c, Factoring Trinomials by Grouping
4.5a, Special Factorizations—Cubes
4.5b, Factoring Expressions by Grouping

Recommended software lessons for review
4.2a, Multiplying Polynomials
4.2b, The FOIL Method
4.4a, GCF of a Polynomial
4.4d, Factoring Trinomials by Trial and Error

The objective here is to use various methods to factor a polynomial completely—that is,
to write it as a product of polynomials in which none of the factors can be factored further.
Trinomials (polynomials with three terms) receive particular emphasis.

Factoring is not an exact science; one can only try different methods, and some polynomials
just do not factor. Fortunately, it is quite easy to check whether a proposed factorization
is correct, for one can simply perform the multiplication and see if it yields the original
polynomial. (To review multiplication of polynomials, see software lessons 4.2a and 4.2b.)
The first step in factoring is to extract the greatest common factor (GCF) of the terms
in the polynomial. A recommended next step is to see if the remaining expression is of
a special form. Is it of the form a² + 2ab + b² or a² − 2ab + b²? Is it a difference of two
squares? A sum or difference of two cubes? In all those cases, familiarity with special
rizations allows one to factor it immediately. Often none of the forms applies, but
the expression is a trinomial. In that case, one tries grouping (also called the ac-method)
or trial and error. These methods can be slow but are more systematic than they might
sound, and if they yield no factorization then the trinomial does not factor with integer
coefficients . Finally, expressions with more than three terms are best treated by grouping.

Typical questions. Given a polynomial, you should be able to choose its complete factorization
from among several given expressions or else select “Not factorable with integer
coefficients.” Working with the text or software will expose you to problems that cover
the entire range of factoring methods, including problems in which the polynomial is not
factorable. Given a polynomial, and given one of the factors in a complete factorization of
it, you should also be able to find the other factor, as in the following:

Example. Consider the polynomial 27x³ +8y³. One of the factors of this polynomial,
when factored completely, is 3x + 2y. Find the other factor.
Solution: 9x² − 6xy + 4y²

Objective 3b. Solve polynomial equations by factoring.

Text section and exercises
4.6, Polynomial Equations and Applications, #11–58

Software lesson
4.6, Solving Equations by Factoring

To solve a polynomial equation, one expands both sides if necessary, moves all terms to
one side (so that the other side is zero), and factors the resulting expression. Starting with
x(x+4) = 2x+3, for example, this yields the equation (x−1)(x+3) = 0. Since a product
is zero exactly when one of the factors is zero, one obtains all solutions by equating the
factors to zero, one at a time, and solving. In the example, the solutions are 1 and −3.
Note that polynomial equations can have several solutions.

Typical questions. Given a polynomial equation, you should be able to carry out this
process and obtain all solutions.

Example. Solve x(x + 2)(3x − 5) = 0.
Solution: 0, −2, and 5/3; or, in set notation, {0,−2, 5/3}

Example. Consider the equation x² + x = 25 + x. One solution of this equation is 5.
Find the other solution.
Solution: −5

Objective 3c. Determine allowed values for rational expressions.

Text section and exercises
5.1, Multiplication and Division of Rational Expressions, #11-30 (state any restrictions
only)

Software lesson
5.1a, Defining Rational Expressions

A rational expression is a fraction whose numerator and denominator are polynomials.
Since division by zero is undefined, the variable in such an expression cannot equal any
values that would cause the denominator to be zero. To find the “restricted values” of the
variable—those for which the expression is not defined—one sets the denominator equal
to zero and solves the resulting equation.

Typical questions. Given a rational expression, find the restricted values of the variable.

Example. Find the restricted values of x for the rational expression
(2x + 8)/(x² + 3x − 10).
Solution: x ≠ −5, x ≠ 2

Objective 3d. Solve equations and inequalities involving rational expressions.

Text section and exercises
5.4, Equations and Inequalities with Rational Expressions, #1–50

Software lessons
5.4a, Solving Equations Involving Rational Expressions
5.4b, Solving Inequalities with Rational Expressions

Recommended software lessons for review
5.1b, Multiplication and Division of Rational Expressions
5.2, Addition and Subtraction of Rational Expressions

To solve an equation involving rational expressions, the main step is to multiply both sides
by the least common denominator of the expressions that appear in it. This produces
a polynomial equation, which one can solve using the methods of Objective 3b. A last
step is to check the proposed solutions by inserting them into the original equation and
discarding those which make a denominator zero.

The same method does not apply to inequalities involving rational expressions; indeed,
multiplying both sides of an inequality by an expression almost always leads to an incorrect
solution. The reason is that the expression can be either positive or negative , depending on
the value of the variable, and hence the process preserves the inequality for some values of
the variable and reverses it for others. Instead: (1) Move all terms to one side (leaving zero
on the other side), combine the terms on that side into a single rational expression, and
factor the numerator and denominator. This step is of course unnecessary if the original
inequality already had a factored rational expression on one side and zero on the other.
(2) Identify all the values of the variable that make the numerator or denominator zero.
(3) Choose test values of the variable, one within each remaining interval on the number
line, and insert them into the factored inequality. The inequality holds or fails throughout
the interval according to whether it holds or fails for the test value. (4) Test the inequality
at the endpoints of the intervals so obtained.

Typical questions. Given an equation involving rational expressions, you should be able to
give the least common denominator (LCD) of the terms in it, give the polynomial equation
that results from multiplying both sides by that LCD, and give all solutions of the original
equation. You should also be able to solve inequalities involving rational expressions and
describe the solution set in all three of the basic ways—algebraically, in interval notation,
and graphically.

Example. Consider the equation 1/(x + 6) − 2/x = 1. Give the least common denominator
(LCD) of the expressions here. Then give the equation that results from
multiplying both sides by that LCD. Finally, give all solutions of the original equation.
Solution: (x + 6)x; x − 2(x + 6) = (x + 6)x; −4,−3

Example. Solve the inequality (x−4)/(x+1)≤0. Give your solution in both algebraic
and interval notation, and graph it.
Solution: −1 < x ≤4; (−1, 4]; graph omitted

Objective 3e. Use rational equations to solve applied problems, including work
and rate problems.

Text section and exercises
5.5, Applications, #1–28

Software lesson
5.5, Applications Involving Rational Expressions

Like other objectives directed at applications, this one addresses all the steps in solving an
applied problem: setting up an equation that captures the given information, solving it,
and interpreting the mathematical solution as it applies to the original problem. Again,
the hardest step is to set up the equation. The key here is to assign a variable name to
the quantity that one is trying to find. The given information says that two things are
equal, and one then focuses on expressing those things in terms of the variable. Rational
expressions arise in several situations. For instance, if a question asks for the speed x at
which a cyclist rides and the given information concerns the time that it takes to ride 20
miles, then one can express that time as 20/x. If a question asks for the number of hours
t that it takes Ann to paint a room and the given information concerns the rate at which
she works, perhaps in the guise of giving the time it takes Ann and some other person to
paint the room when working together, then one can express Ann’s contribution to the
total rate as 1/t rooms per hour.

Typical questions. Each exam question addresses either just one part of the process (setting
up an equation in an applied problem or using an equation that is already set up to solve
the problem) or it addresses the entire process.

Example. Fred takes three times as long as Jake to mow a lawn. Working together,
they can mow the lawn in 75 minutes. Give an equation that one could solve to
determine the number of minutes t that it takes Jake to mow the lawn.
Solution: 1/t + 1/(3t) = 1/75

Example. Ann rows 4 mph in still water. On a certain river, it takes her the same
time to row 3 miles upstream as it takes to row 7 miles downstream. Let x be the
speed of the current. The given information can be summarized in the equation
3/(4 − x) = 7/(4 + x). Find the speed of the current. Round your answer to the
nearest tenth of a mile per hour.

Solution: 1.6 mph

Example. Todd takes twice as long as Sue to paint a room. Together they can paint
the room in 2 hours. How long would it take Sue to paint it by herself?
Solution: 3 hours

Unit 4. Radical Expressions and Rational Exponents

Objective 4a. Simplify radical expressions, including rationalizing denominators.
Text section and exercises

6.1, Roots and Radicals, #11–62
Software lessons

6.1b, Simplifying Radicals
6.1c, Division of Radicals

Recommended software lesson for review
1.7, Simplifying Integer Exponents I
6.1a, Evaluating Radicals

To simplify a radical expression means to achieve three things. First, an expression under
an nth-root sign should have no perfect nth powers as a factor. One can achieve that by
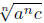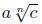writingas if n is odd or a is positive, or writing it as 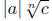if n is even and
a could be negative. The second condition is that radical signs should not appear in a
denominator. One can achieve that by rationalizing the denominator, as described in the
text and software. Finally, there should be no quotients within the radical sign. One can
achieve that by writing 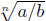as n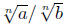 and then rationalizing the denominator.
Typical questions. You should be able to simplify a radical expression in the ways just
described. In particular, you should be able to rationalize a denominator.

Example. Simplify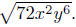 Assume that the variables may be positive or negative.
Solution: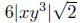

Example. Simplify 3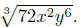
Solution: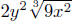

Example. Simplify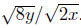 Assume that the variables are positive.
Solution: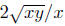

Example. Simplify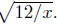 Assume that x is positive.
Solution: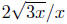

Objective 4b. Convert expressions from radical form to rational-exponent
form and vice versa, and simplify expressions involving integer and rational
exponents.

Text sections and exercises
1.8, More on Exponents, #1–32
6.2, Rational Exponents, #1–25, 41–91

Software lessons
1.8a, Simplifying Integer Exponents II
6.2, Rational Exponents

Recommended software lesson for review
1.7, Simplifying Integer Exponents I

Rational exponents provide an alternate way to write expressions involving nth roots.
The notation a^1/n means 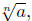and more generally a^m/n means .These definitions
are motivated by the basic properties of integer exponents, such as a^pa^q = a^p+q and
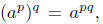and those properties continue to hold in this expanded setting. To review
them, see software lessons 1.7 and 1.8a. Just as with radicals of even index, raising a
negative number to a power m/n does not make sense as a real number when n is even.
The objective here is to convert between radical and rational-exponent notation and to
simplify expressions involving integer and rational exponents—that is, to write them so
that each variable appears no more than once in a product or quotient, where it is raised
to a positive power. Some problems combine these processes by asking you to write a
complicated radical expression in rational-exponent form and simplify the result.

Typical questions. You should be able to write a radical expression in terms of rational exponents,
write an expression involving rational exponents in terms of radicals, and simplify
an expression that involves rational exponents.

Example. Change 3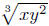into an equivalent expression in exponential notation.
Solution: x^1/3y^2/3 and 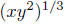are both correct.

Example. Change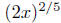 into an equivalent expression in radical notation.
Solution: 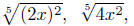and 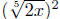are all correct.

Example. Simplify .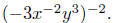
Solution: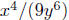

Example. Simplify 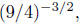or say “not a real number.”
Solution: 8/27

Example. Simplify 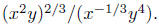Use positive exponents only.
Solution: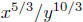

Example. Change 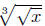to exponential notation, and simplify.
x^1/6

Objective 4c. Add, subtract, multiply, and divide radical expressions.

Text section and exercises
6.3, Arithmetic with Radicals, #1–60

Software lessons
6.3a, Addition and Subtraction of Radicals
6.3b, Multiplication of Radicals

To add or subtract radicals, one simplifies each individual radical and combines like terms.
Simplifying the terms in
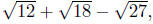, for example, yields 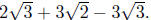Since
the first and last are like terms this sum simplifies to 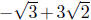but no further; simplified
radical terms with different radical parts just do not combine.

In performing arithmetic with radicals, one also encounters products of radicals. The rule
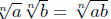allows one to simplify such expressions. Some problems, such as simplifying
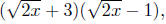involve both this process and adding or subtracting radicals.

The present objective includes one further specialized technique. When the denominator
of a quotient is a sum or difference of square roots, one can rationalize it by multiplying
the numerator and denominator by the difference or sum, respectively, of the square roots.
Typical questions. You should be able to simplify radical expressions that involve addition,
subtraction, multiplication, or division. You should also be able to rationalize a
denominator that is a sum or difference of square roots.

Example. Simplify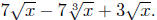
Solution: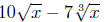

Example. Simplify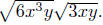 Assume that both variables are positive.
Solution: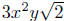

Example. Simplify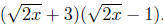
Solution: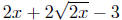

Example. Simplify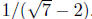
Solution: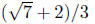

Unit 5. Quadratic Equations and Their Applications

Objective 5a. Solve quadratic equations using factoring, square roots, completing
the square, and the quadratic formula.

Text sections and exercises
7.1, Quadratic Equations: Completing the Square, #1–12, 16–21, 26–31, 34–38, 44-48
7.2, Quadratic Equations: The Quadratic Formula, #25–40, 43, 45, 49, 53, 57, 59

Software lessons
7.1a, Quadratic Equations: The Square Root Method
7.1b, Quadratic Equations: Completing the Square
7.2, Quadratic Equations: The Quadratic Formula

A quadratic equation is a polynomial equation that involves the square of the variable
but no higher powers. In this objective, we find the solutions of quadratic equations.
Sometimes the solutions are real numbers, and sometimes they are nonreal.

The text and software present four basic ways to solve quadratic equations: factoring (as
in Objective 3b), taking square roots, completing the square, and using the quadratic
formula. A good strategy for solving such equations is to use factoring or square roots
when the form of the equation suggests those methods and otherwise fall back on the
quadratic formula. Nevertheless, completing the square is important (as in Objective 7a
below), and some questions will ask about it.

Typical questions. You should be able to find all real solutions of a given quadratic equation.
Usually the method will be up to you. However, you will also be asked about
completing the square.

Example. Solve (x + 1)² = 25. If there is more than one solution, separate solutions
with a comma. If solutions are nonreal, say “no real solutions.” Express your answers
as numbers, not as equations.
Solution: 4, −6

Example. Solve 9x² = 6x − 1. If there is more than one solution, separate solutions
with a comma. If solutions are nonreal, say “no real solutions.” Express your answers
as numbers, not as equations.
Solution: 1/3

Example. Completing the square for 2x² +12x−6 = 0 yields which of the following?
(a) (2x + 3)² = 15 (b) (x + 3)² = 12 (c) (x + 6)² = 42 (d) 2(x + 3)² = 15
Solution: (b)

Objective 5b. Use the discriminant to classify the solutions of a quadratic
equation.

Text section and exercises
7.2, Quadratic Equations: The Quadratic Formula, #1–12

Software lesson
7.2, Quadratic Equations: The Quadratic Formula

The expression b² − 4ac that appears within the radical in the quadratic formula is called
the discriminant of the expression ax² + bx + c. If the discriminant is positive, then the
equation ax² + bx + c = 0 has two real solutions; if the discriminant is zero, then the
equation has one real solution; if the discriminant is negative, then the equation has two
nonreal solutions (and, in each case, no other solutions).

Typical questions. You should be able to compute the discriminant of a given quadratic
expression. Also, given the discriminant of an expression ax² +bx+c, you should be able
to determine how many real and nonreal solutions the equation ax² + bx + c = 0 has.

Example. Find the discriminant of the quadratic expression 2x² − 3x − 4.
Solution: 41

Example. Consider the quadratic equation 17x² − 37x + 26 = 0. The discriminant
of the quadratic expression here is −399. Which of the following best describes the
solutions of this equation?

(a) One real solution (b) Two distinct real solutions (c) Two nonreal solutions
Solution: (c)

Objective 5c. Use quadratic equations to solve applied problems, including
Pythagorean theorem, projectile motion, geometry, work, and rate problems.

Text section and exercises
7.3, Applications, #1–50

Software lesson
7.3, Applications (Quadratic)

Again, this objective addresses all the steps in solving an applied problem: setting up an
equation that captures given information, solving it, and interpreting the solution as it
applies to the original problem. Again, a key is to assign a variable name to the quantity
that one is trying to find; one can then focus on stating the given information as an
equation involving that variable. Some problems require the Pythagorean theorem, which
states that the square of the hypotenuse in a right triangle equals the sum of the squares
of the legs.

A mathematical solution might not be meaningful in the original problem. For example,
in a problem about the time it takes to do a certain job, the appropriate equation might
have two solutions, one positive and one negative, but doing a job in a negative amount
of time makes no sense. One should always check whether each mathematical solution
actually solves the applied problem.

Typical questions. Each exam question addresses either just one part of the process (either
setting up an equation in an applied problem or using an equation that is already set up
to solve the problem) or it addresses the entire process.

Example. One leg of a right triangle is 4 inches shorter than the other. The hypotenuse
of the triangle is 20 inches. Find the length of the shorter leg. Round your answer to
the nearest tenth of an inch.
Solution: 12 inches

Example. A rectangle is 5 meters longer than it is wide. Increasing the length and
width of the rectangle by 3 meters doubles its area. If w is the width of the original
rectangle, then the equation (w+3)(w+8) = 2w(w+5) summarizes this information.
Find the width of the original rectangle. Round your answer to the nearest tenth of
a meter.
Solution: 5.4 meters

Objective 5d. Solve radical equations.

Text section and exercises
7.4, Equations with Radicals, #1–44

Software lesson
7.4, Solving Radical Equations

To solve an equation involving radicals, one first isolates a radical term, moving it to one
side of the equation and moving all other terms to the other side. If the radical is a square
root, one then squares both sides of the equation; if it is a cube root, one cubes both sides,
etc. This process usually produces a polynomial equation, which one can solve by methods
discussed in earlier objectives. Occasionally, the resulting equation still includes a radical,
and one must repeat the process in order to obtain a polynomial equation. In all cases an
important final step is to check the possible solutions so obtained, for raising both sides of
an equation to a power can introduce extraneous solutions.

Typical questions. You should be able to find all solutions of a radical equation.
Example. Solve the equation.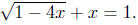
Solution: 0, −2

Example. Consider the equation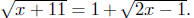 After clearing radicals, this
becomes the quadratic equation x² −30x+125 = 0. Find the solutions of the original
radical equation.
Solution: 5

Objective 5e. Solve polynomial and rational equations that become quadratic
after substitution or rearrangement.

Text section and exercises
7.5, Equations in Quadratic Form, #1–4, 9, 11–30, 37, 41–50

Software lesson
7.5, Equations in Quadratic Form

Some equations, while not quadratic, can be solved by means of a related quadratic equation.
The two main kinds are rational equations that become quadratic after denominators
are cleared, and equations for which a “substitution” yields a quadratic equation in a new
variable. If the original variable is x, then to substitute means to assign a variable name,
say u, to an expression involving x and write the equation in terms of u alone. By solving
that equation for u, plugging the solutions back into the relation defining u, and solving,
one finds the solutions x of the original equation.

Typical questions. You should be able to solve rational equations that become quadratic
after clearing denominators. Exam questions about substitution will address one or more of
the fours steps in the process: identifying a useful substitution, writing the given equation
in terms of the new variable u, solving for u, and deducing the solutions of the original
equation.

Example. Solve the equation 2/(x − 1) = 1 + 5/x.
Solution: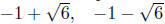

Example. Consider the equation x⁴−6x²+8 = 0. Give a substitution that transforms
this to a quadratic equation for a variable u. State that equation, and give the solutions
u. Finally, give the solutions x of the original equation.
Solution: u = x²; u² − 6u + 8 = 0; 4, 2; 2, −2,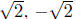

Unit 6. Parabolas, Quadratic Inequalities, Distance, and Circles

Objective 6a. Graph quadratic functions given either in standard form or in
the form y = a(x − h)² + k.

Text section and exercises
8.1, Quadratic Functions: Parabolas, #21–24, 25–40 (vertex and graph only)

Software lesson
8.1, Graphing Parabolas

The term “function,” which the text and software use in this unit, simply means a process
or rule by which an input determines an output. A quadratic function is one defined by a
rule y = ax² +bx+c, where a, b, and c are constants and a 6= 0; here one inputs a number
x and gets an output y. We do nothing with functions in this unit other than using the
word in discussions; in particular, we are not interested in the general concepts of domain
and range of a function, nor with what is called functional notation.

A graph y = ax² + bx + c has a particular U shape, called a parabola, opening upward
if a is positive and downward if a is negative. The key to graphing a parabola is to find
the low or high point of the U, called the vertex of the parabola; once one has plotted the
vertex and one or two other points, a freehand sketch yields a fairly accurate graph. In
turn, the key to finding the vertex is to rewrite ax² + bx + c in the form a(x − h)² + k by
completing the square. The vertex of the parabola is then the point (h, k). The parabola
is wide if |a| is small and narrow if |a| is large.

Typical questions. Given an equation in the standard form y = ax² + bx + c, you should
be able to complete the square to obtain the form y = a(x−h)² +k, give the vertex of the
parabola, say whether it opens upward or downward, and say whether it is narrower or
wider than some other given parabola. You should also be able to choose the correct graph
from among several sketched. Conversely, given a graph, you should be able to choose the
correct equation from among several proposed equations.

Example. Complete the square in the equation y = 2x² + 4x + 9. Give the vertex of
the parabola, and say whether it opens upward or downward.
Solution: y = 2(x + 1)² + 7; (−1, 7); upward

Objective 6b. Find the x-intercepts of the graph of a quadratic function.

Text section and exercises
8.1, Quadratic Functions: Parabolas, #25–40 (zeros only)

Software lesson
8.1, Graphing Parabolas

The graph of a quadratic function y = ax² + bx + c can intercept the x-axis in zero, one,
or two points. Since those x-intercepts are the points at which y = 0, one can find them
by solving the equation ax² +bx+c = 0. The process is even easier for an equation of the
form y = a(x − h)² + k, since in that case one can use the square-root method.

Typical questions. You should be able to find the x-intercepts, if any, of a parabola given
in either of the forms y = ax² + bx + c or y = a(x − h)² + k.

Example. How many x-intercepts does the graph y = 2x² + 3x + 4 have?
Solution: None

Example. Find all x-intercepts of the graph y = 2(x − 1)² − 8.
Solution: −1 and 3

Objective 6c. Solve quadratic inequalities.

Text section and exercises
8.2, Quadratic Inequalities, #1–50

Software lesson
8.2, Solving Quadratic Inequalities

The method for solving quadratic inequalities is like that for solving rational inequalities
(see Objective 4b). One first moves all terms to one side, leaving zero on the other. The
solutions of the corresponding equation then cut the real number line into intervals, and
by choosing test values of the variable one can determine whether the inequality holds
throughout each interval or fails throughout. The final step of determining whether a
solution interval includes its endpoints is easier than before: If the inequality is ≥or≤,
then endpoints are included, and if it is > or < they are not.

Typical questions. You should be able to solve a quadratic inequality and describe the
solution set in all three basic ways—algebraically, in interval notation, and graphically.

Example. Solve the inequality x² + 4x − 5 ≥0. Give your solution in both algebraic
and interval notation, and graph it.
Solution: x ≤−5 or x  ≥1; (−∞,−5] ∪[ [1,∞); graph omitted

Example. Solve the inequality x² > 2x − 3. Give your solution in both algebraic and
interval notation, and graph it.
Solution: All real numbers; (−∞,∞); graph omitted

Objective 6d. Use the distance formula to find the distance between any two
points in a plane.

Text section and exercises
8.5, Distance Formula and Circles, #1–12, 49

Software lesson
8.5, Distance Formula and Circles

The distance between any two points in a plane is determined using the distance formula,
which is itself an application of the Pythagorean theorem that we have used previously.
For points (x₁, y₁) and (x₂, y₂), the distance formula is

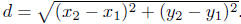
Typical questions. Given two points, you should be able to find the distance between
them.

Example. Find the distance between (−1, 6) and (2,−5).
Solution: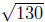

Objective 6e. Graph circles given equations in either standard form or expanded
form and determine the equations of given circles.

Text section and exercises
8.5, Distance Formula and Circles, #13–48

Software lesson
8.5, Distance Formula and Circles

A circle is the set of all points in a plane that are a fixed distance, called the radius, from
a fixed point, called the center. From the distance formula we can determine that the
standard form for the equation of a circle is (x − h)² + (y − k)² = r², where the circle
has center at (h, k) and a radius of r. If the equation of a circle is given in the form
x²+y²+ax+by = c, then it must be rewritten in standard form by completing the square
in x and also in y.

Typical questions. Given the equation of a circle, you should be able to determine its
center and radius. Conversely, given the center and radius of a circle, you should be able
to create the equation of that circle in standard form.

Example. Find the equation of the circle with center (−2, 5) and radius 3.
Solution: (x + 2)² + (y − 5)² = 9

Example. Write the equation of the circle x² + y² − 4x + 10y = 7 in standard form
and identify the center and radius of the circle.
Solution: (x − 2)² + (y + 5)² = 36, center (2,−5), radius 6