Get it on Google Play Get it on Apple Store

COLLEGE ALGEBRA

COURSE NUMBER: MATH-105 COURSE TITLE: College Algebra

CREDIT HOURS: 3

INSTRUCTOR: Ryan Willis

OFFICE LOCATION: 203 Arts and Sciences Building

PHONE: 620-251-7700 ext. 2164

OFFICE HOURS: See schedule posted on the office door

PREREQUISITE(S):
A minimum score of 45 on the Algebra Test of the COMPASS or
credit in Intermediate Algebra.

REQUIRED TEXT
AND MATERIALS:
Algebra for College Students, 5th Edition by Mark Dugopolski

COURSE
DESCRIPTION:
Topics included in the course are quadratic equations, ratio,
proportion and variation , complex numbers, determinants, and
elimination theory and inequalities .

EXPECTED LEARNER
OUTCOMES:
Upon completion of this course, the student will be able to:
1. Understand the basic rules of Algebraic Expressions.
2. Solve given linear and quadratic equations.
3. Understand linear and quadratic relations and functions.
4. Understand exponential and logarithmic functions.
5. Solve given systems of equations .
6. Understand elementary probability and statistics.

LEARNING TASKS
& ACTIVITIES:
The class will meet during the scheduled class time for recitation
and discussion of selected chapters from the text. A traditional
lecture approach will be used. Homework regarding the discussed
material will be assigned at the end of each class period. Periodic
quizzes may also be given to assess comprehension.
Unit I, Chapter 1: 1.3-1.6, Chapter 5: 5.1-5.7, Chapter 6: 6.1-6.5,
Chapter 7: 7.1-7.4
Unit II, Chapter 2: 2.1-2.4
Unit III, Chapter 3, Chapter 9, Chapter 12: 12.2-12.4
Unit IV, Chapter 11
Unit V, Chapter 4, Chapter 12: 12.1
Unit VI, Chapter 13: 13.5, Chapter 14: 14.1-14.3

ASSESSMENT OF
OUTCOMES:
Grades of A (90-100), B (80-89), C (70-79), D (60-69), and
F (0-59) are given in this course. An incomplete is given if
previously agreed upon by the instructor with a specific time
designated for the completion of the incomplete work. Please note
the college’s policy on incompletes as stated in the college catalog.

Tests MUST be taken on the scheduled day and during the regular
class period. ONLY if arrangements are made with the instructor
PRIOR to the original test date will a student be allowed to take
the test early. Due to abuse in the previous policy, no student will
be allowed to makeup a test. Current policy allows each student
one drop test to accommodate unforeseen circumstances and the
subsequent failure to be tested on the scheduled test date.

A student’s final course grade will be based upon homework,
quizzes and exams. Partial credit is given on exams so show all
work. In the event that there would be extra credit given on a test,
partial credit is not given in the extra credit problems. There will
be approximately 6 tests with the lowest test dropped.

LATE TESTS ARE NOT GIVEN. IF YOU MISS A
TEST IT COUNTS AS YOUR DROPPED TEST AT
THE END OF THE SEMESTER. IF YOU ARE
GOING TO BE ABSENT DURING TEST DAY DUE
TO A COLLEGE EVENT YOU MUST TAKE THE
TEST EARLY.

ATTENDANCE
POLICY:
Attendance in a math course is essential for any degree of success
in that course. When it is determined that lack of attendance is
jeopardizing the success of the student, counseling will be in order
to conclude whether the student should remain enrolled in the
class. The student should not miss class periods for a course of
this type. In each class period new ideas are presented which build
upon the ideas of the previous class period. These ideas, in turn,
lay the foundation for what will be discussed at the next class
period. When a student is absent all information should be
obtained from a fellow student concerning the assignment covered
and to be covered. Absence is no excuse for being unaware of the
progress and activities of the class. Attendance is expected for
success in the class, but attendance will not be taken explicitly.

NOTICE:
Out of respect for your classmates, when you enter the classroom
please turn off your cell phone. Remember that your time in the
class should be spent listening; not taking calls. Thank you.

This syllabus is subject to revision with prior notification to the student by the
instructor.

COMPETENCIES:
UNIT I
The student will understand the basic rules of algebraic expressions.

1. Define:
a. Naturals
b. Wholes
c. Integers
d. Rationals
e. Irrationals
f. Reals

2. Given a number identify the sets from objective 1 to which the number belongs

3. Define:
a. an where a∈R , n∈N
b. a-n where a∈R , a ≠ 0 , n∈N
c. a0 where a∈R
d. 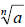where a∈R , n∈N
e. 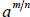where a∈R , m /n∈Q

4. State and prove the exponent rules for natural number exponents
5. Simplify given exponent phrases
6. List the properties of real numbers by name and symbolic representation
7. Given a statement list the properties of real numbers being illustrated
8. Simplify a given statement using properties of real numbers
9. Define polynomial
10. Perform operations on given polynomials
11. Factor a given polynomial
12. Define the addition, subtraction , multiplication, and division of rational expressions
13. Perform operations on given rational expressions
14. State and prove the Rules for Radicals.
15. Simplify a given phrase containing radicals
16. List the components of a Logic Structure
17. State the Binomial Theorem

UNIT II

The student will solve given linear and quadratic equations.

1. Define:
a. linear equation in one variable
b. complex numbers
c. quadratic equation in one variable
2. Solve a given linear equation
3. Perform operations on complex numbers
4. State and prove the quadratic formula
5. Solve a given quadratic equation
6. Work word problems using the above concepts

TEXT: Chapter 1:85-180

UNIT III
The student will understand linear and quadratic relations and functions.

1. Define
a. Relation
b. Function
c. Linear Relation
d. Quadratic Function
e. Slope

2. State that the graph of a
a . linear relation is a straight line
b. quadratic relation is a parabola

3. State and prove: If y = mx + b then m is the slope and b is the y intercept
4. Graph a line given information about it
5. Find the slope of a line given information about it
6. Write the equation of a line given information about it
7. State and prove:
a. If y = a(x − h)2 + k then the vertex is (h, k)
b. If y = ax2 + bx + c then the x coordinate of the vertex is − b /2a
8. Write the equation of a parabola given information about it
9. Given the equation of a parabola find the vertex and graph it
10. Work word problems using the above concepts

UNIT IV
The student will understand exponential and logarithmic functions.

1. Define exponential function
2. Evaluate given:
a. exponential expressions
b. exponential functions
3. Graph given exponential functions
4. Solve given exponential equations
5. Define logarithmic function
6. State and prove the seven properties of logarithms
7. Given an exponential equation write the corresponding logarithmic equation
8. Given an logarithmic equation write the corresponding exponential equation
9. Evaluate given logarithmic expressions
10. Simplify given log statements using objective 6
11. State and prove that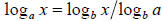
12. Solve given logarithmic equations
13. Work word problems using the above concepts

UNIT V
The student will solve given systems of equations.

1. Solve Systems of linear equations using:
a. substitution
b. addition
c. Gauss-Jordan
d. Cramer's Rule

2. Define
a. matrix
b. determinant

3. Find the determinant of a given matrix
4. Solve given linear programming problems

UNIT VI
The student will understand elementary probability and statistics.

1. Define
a. Pascal's Triangle
b. n!
c. l!
d. 0!
e.

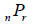
2. State the Binomial Theorem
3. Expand a given expression of the form (x + y)n using objective 2
4. Find the rth term of a given binomial expansion
5. State the fundamental principle of counting
6. Define:
a. independent events
b. p(n,r)

7. Find the number of ways a given event can occur

8. Evaluate:
a. p(n,r)
b.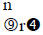

9. Define probability of Event E.

10. State:
a.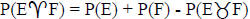
b. Five properties of probabilities

11. Find the probability that a given event will occur

This syllabus is subject to revision with prior notification to the student by the
instructor.

Prev Next