College Algebra

1 Laws of algebra

1.1. Terminology and Notation . In this section we review the notations
used in algebra. Some are peculiar to these notes. For example the notation
A := B indicates that the equality holds by definition of the notations in-
volved. (See for example Paragraph 1.2 which follows.) Two other notations
which will become important when we solve equations are => and .
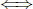The notation P => Q means that P implies Q i.e. "If P, then Q". For
example, x = 2 => x² = 4. (Note however that the converse satement
x² = 4 => x = 2 is not always true since it might be that x = -2.) The
notation P 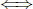Q means P => Q and Q => P, i.e. "P if and only if
Q". For example 3x - 6 = 0 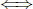x = 2. The notations => and
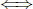
are explained more carefully in Paragraphs 8.2 and 8.3 below.

1.2. Implicit Multiplication. In mathematics the absence of an operation
symbol usually indicates multiplication: ab mean a × b. Sometimes a dot
is used to indicate multiplication and in computer languages an asterisk is
often used.

ab := a · b := a * b := a× b

1.3. Order of operations . Parentheses are used to indicate the order
of doing the operations: in evaluating an expression with parentheses the
innermost matching pairs are evaluated first as in



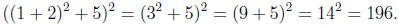
There are conventions which allow us not to write the parentheses. For
example, multiplication is done before addition

ab + c means (ab) + c and not a(b + c).

and powers are done before multiplication:

ab²c means a(b²)c and not (ab)²c:

In the absence of other rules and parentheses , the left most operations are
done first.

a - b - c means (a - b) - c and not a - (b - c):

The long fraction line indicates that the division is done last:

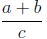means (a + b)/c and not a + (b/c):

In writing fractions the length of the fraction line indicates which fraction is
evaluated first:

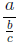means a/(b/c) and not (a/b)/c,

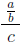means (a/b)/c and not a/(b/c).

The length of the horizontal line in the radical sign indicates the order of
evaluation:

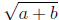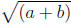means and not :
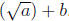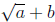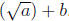means and not :

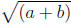1.4. The Laws of Algebra. There are four fundamental operations which
can be performed on numbers.

1. Addition. The sum of a and b is denoted a + b.

2. Multiplication. The product of a and b is denoted ab.

3. Reversing the sign. The negative of a is denoted -a.
4. Inverting. The reciprocal of a (for a ≠ 0) is denoted by a^-1 or by
.
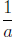
These operations satisfy the following laws.

Associative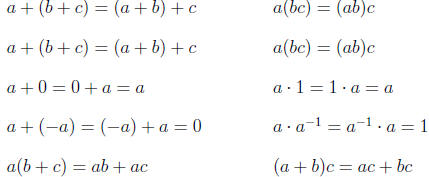
Commutative
Identity
Inverse
Distributive

The operations of subtraction and division are then defined by

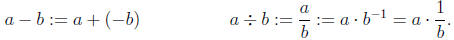All the rules of calculation that you learned in elementary school follow from
the above fundamental laws. In particular, the Commutative and Associative
Laws say that you can add a bunch of numbers in any order and similarly
you can multiply a bunch of numbers in any order. For example,

(A+B)+(C+D) = (A+C)+(B+D), (A · B) (C · D) = (A · C) (B · D).

1.5. Because both addition and multiplication satisfy the commutative, as-
sociative, identity, and inverse laws, there are other analogies:

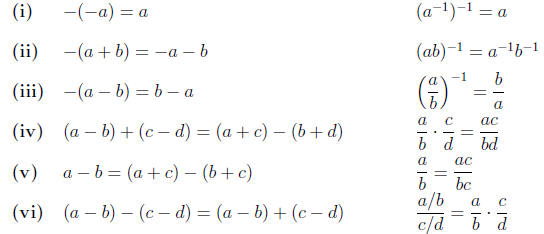These identities are proved in the Guided Exercises. (An identity is an
equation which is true for all values of the variables which appear in it.)

1.6. Here are some further identities which are proved using the distributive
law.

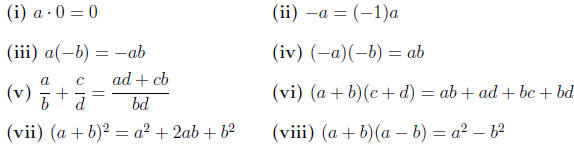These are also proved in the Guided Exercises.

1.7. The following Zero-Product Property will be used to solve equations.

pq = 0 p = 0 or q = 0 (or both).

Proof: If p = 0 (or q = 0) then pq = 0 by (i) in Paragraph 1.6 . Conversely,
if p ≠ 0 then q = p^-1pq = p^-10 = 0.

definition 1.8. For a natural number n and any number a the nth power
of a is

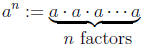
The zeroth power is

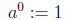
and negative powers are defined by

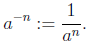
1.9. The following laws are easy to understand when m and n are integers.
In Theorem 4.1 below we will learn that these laws also hold whenever a
and b are positive real numbers and m and n are any real numbers, not just
integers.

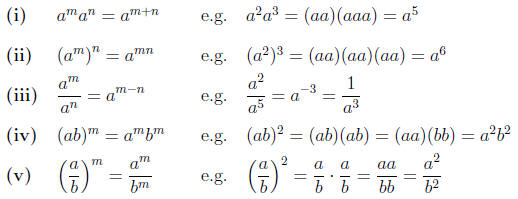2 Kinds of Numbers

2.1. We distinguish the following different kinds of numbers.

• The natural numbers are 1, 2, 3 ...

• The integers are... - 3,-2,-1, 0, 1, 2, 3...

• The rational numbers are ratios of integers like 3/2, 14/99, -1/2.

• The real numbers are numbers which have an infinite decimal expan-
sion like

•The complex numbers are those numbers of form z = x + iy where
x and y are real numbers and i is a special new number called the
imaginary unit which has the property that

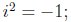Every integer is a rational number (because n = n/1), every rational number
is a real number (see Remark 2.3 below), and every real number is a complex
number (because x = x + 0i). A real number which is not rational is called
irrational.

2.2. Each kind of number enables us to solve equations that the previous
kind couldn't solve:

• The solution of the equation x + 5 = 3 is x = -2 which is an integer
but not a natural number.

• The solution of the equation 5x = 3 is 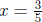which is a rational number
but not an integer.

• The equation x² = 2 has two solutions 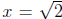. The number 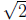is a
real number but not a rational number. (See Remark 2.5 below.)

• The equation x² = 4 has two real solutions x = ±2 but the equation
z²= -4 has no real solutions because the square of a nonzero real
number is always positive. However it does have two complex solutions,
namely z = ±2i.

We will not use complex numbers until Section 20 but may refer to them
implicitly as in

The equation x² = -4 has no (real) solution.

Remark 2.3. It will be proved in Theorem 24.6 that a real number is rational
if and only if its decimal expansion eventually repeats periodically forever as
in the following examples:

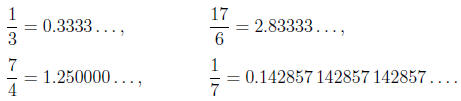
Remark 2.4. Unless the decimal expansion of a real number is eventually
zero, as in 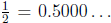:, any finite part of the decimal expansion is close
to, but not exactly equal to, the real number. For example 1.414 is close to
the square root of two but not exactly equal:

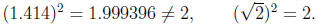
If we compute the square root to more decimal places we get a better ap-
proximation, but it still isn't exactly correct:

(1.4142135623730951)² = 2.00000000000000014481069235364401.

Remark 2.5. Here is a proof that the square root of 2 is irrational. If it
were rational there would be integers m and n with

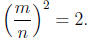
By canceling common factors we may assume that m and n have no common
factors and hence that they are not both even. Now m² = 2n² so m² is even
so m is even, say m = 2p. Then 4p² = (2p)² = m² = 2n² so 2p² = n² so n²
is even so n is even. This contradicts the fact m and n are not both even.