Completing the Square
Completing the square is a technique that can be
applied to an equation in-
volving a variable squared. This technique allows you to rewrite the equation so
that
it involves a "perfect- square trinomial ", i.e. a polynomial that can be factored
as a
single factor squared. This technique is used to:
• Solve quadratic equations.
• Write conic equations (parabolas, circles, etc.) in standard form.
• Rewrite integrals in order to do trig substitutions .
To complete the square, start with a quadratic polynomial in the form
ax2 + bx + c,
where a, b, and c are real numbers and a ≠ 0.
1. If a ≠ 1, then we need to factor a out of the first two terms of the
polynomial
so that the coefficient of x 2 is one. When you write the polynomial
down, leave
room between the x term and the constant term.
2. To figure out what to add and subtract from the equation , take the
coefficient
of x divide it by 2 and square it. Then, add and subtract this term from your
polynomial in the space you left, inside the parentheses if there are any.
3. The first three terms of the polynomial will factor as a perfect square , and
the
last two terms can be combined into one term . If you had to factor out in Step
1, you will need to move the subtracted term to the outside of the parentheses.
Example 1 Complete the square: x2 - 4x - 2
1. The coefficient of x2 is already one.
2. The coefficient of x is -4. Dividing this by 2, we get -2. Squaring -2, we
get
4. So, we add and subtract 4 from our equation:
x2 - 4x + 4 - 4 - 2
3. Simplifying , we have: (x - 2)2 - 6.
So, x2 - 4x - 2 = (x - 2)2 - 6.
Example 2 Complete the square: 2x2 + 4x + 3
1. Factoring 2 out of the first two terms and leaving room, we have:
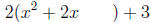
2. After factoring, the coefficient of x is 2. Dividing
this by 2, we get 1. Squaring
1, we get 1 again. So, we add and subtract 1 from our equation:
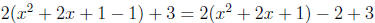
3. Simplifying, we have: 2(x + 1)2 + 1.
So, 2x2 + 4x + 3 = 2(x + 1)2 + 1.
Example 3 Solve x2 + 6x - 1 = 0 by completing the square.
1. We do not need to factor out because the coefficient of x2 is
already one.
2. The coefficient of x is 6. Dividing this by 2, we get 3. Squaring 3, we get
9. So,
we add and subtract 9 from our equation, or, equivalently , you could add 9 to
both sides of the equation.
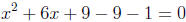
3. Simplifying, we have: (x + 3)2 - 10 = 0.
Now, we can solve for x by getting the square term by itself and taking the
square root
of both sides of the equation.
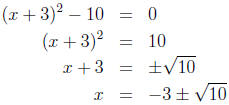
Now, check the answers:
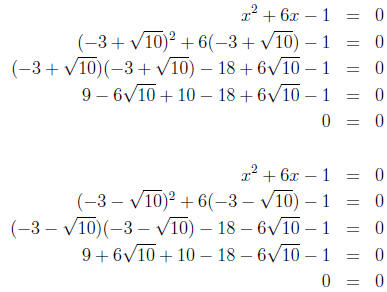
So, the solutions to x2 + 6x - 1 = 0 are
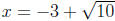and 
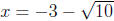
Example 4 Write the quadratic equation 2x2
+ 6x + 3y = 3 in standard form.
Standard form of a quadratic equation is y = a(x - h)2 + k. This
would be graphed
as a parabola with vertex (h, k) and axis x = h. If a > 0, the parabola opens
up, and,
if a < 0, the parabola opens down.
1. We do need to factor out because the coefficient of x2 is 2, so
factor 2 out of the
x2 and x terms. Doing this, and moving the 3 to the left-hand side,
we have:
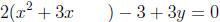
2. The coefficient of x is 3. Dividing this by 2, we get
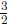. Squaring
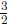, we get 
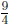. So,
we add and subtract 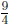from our equation.
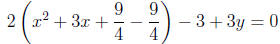
Moving th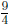e -
to the
outside of the parentheses, we have:
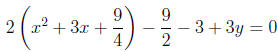
3. Simplifying, we have:
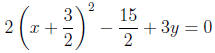
Now, we can solve for y in the equation to find the standard form.
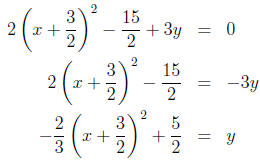
So, the standard form for the quadratic equation is:
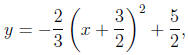
and this is a parabola with vertex
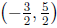and axis 
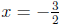. The parabola is opening
down because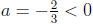 
.
Example 5 Write the circle x2 + y2
- 6x + 4y + 4 = 0 in standard form.
Standard form of a circle is (x - h)2 + (y - k)2 = r2,
where the center of the circle
is at the point (h, k) and the radius of the circle is r. We will need to
complete the
square twice, once for x and once for y.
1. We do need to factor out because the coefficients of x2 and y2
are one. We may
want to rearrange the terms and leave space to make our calculations easier:
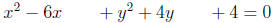
2. The coefficient of x is -6. Dividing this by 2, we get
-3. Squaring -3, we get
9. So, we add and subtract 9 from our equation.
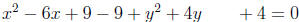
The coefficient of y is 4. Dividing this by 2, we get 2.
Squaring 2, we get 4. So,
we add and subtract 4 from our equation.
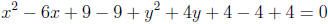
3. Simplifying, we have:
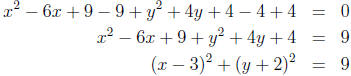
So, the standard form for the circle is:
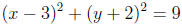
The center of the circle is at (3,-2) and the radius is 3.
Example 6 Integrate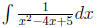 
The idea here is to complete the square in the denominator
so that this will look like
the derivative of the inverse tangent function:
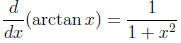
1. The coefficient of x2 is already one.
2. The coefficient of x is -4. Dividing this by 2, we get -2. Squaring -2, we
get
4. So, we add and subtract 4 from our equation:
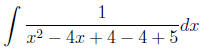
3. Simplifying, we have:
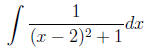
If we let u = x - 2, then du = dx, and we can make the
u-substitution. The integral
becomes:
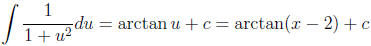
So,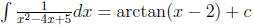
.
Problems to try!
1. Solve x2 + 8x + 3 = 0
2. Solve 3x2 - 1 = 6x
3. Solve 2x2 - 2x + 5 = 0
4. Write the quadratic equation y = 2x2 - 20x + 54 in standard form.
5. Write the circle 4x2 + 4y2 + 8x - 56y + 191 = 0 in
standard form.
6. Integrate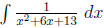 
using the integration formula :
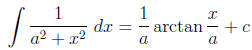
Answers
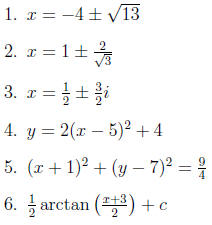
| Prev | Next |