COT3100 Practice Problems for Exam 1
These problems are only meant to help you prepare the
first exam. It is not guaranteed
that the exam questions will be similar to these problems.
There will be five problems on the exam:
1. Propositional logic and equivalences (1.1 and 1.2)
2. Predicates and Quantifiers (1.3)
3. Rules of Inference and Proofs (1.5)
4. Set Operations (2.1 and 2.2)
5. Functions and sequences (2.3 and 2.4)
The (brief) solutions will be available only after 9pm on Thursday night.
However,
instead of memorizing the solutions, you should attempt to solve all problems by
yourself first.
1. What is the truth value of (p 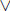 q) → (p
q) → (p
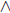 q), when both p and q are false?
q), when both p and q are false?
Solution: You should work out this problem and convince yourself that
your answer is correct.
2. State the converse and contrapositive of, "If I answer this question, then I
will get 4 points".
Solution: You just need to know the definitions of converse and
contrapositive.
Check out the textbook or lecture slides.
3. Which rule of inference allows you to conclude, "Mark has stripes" from
the statements, "Every zebra has stripes" and "Mark is a zebra"?
Solution: Same as above.
4. Construct the truth table for the proposition
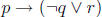 .
.
Solution: Clock yourself to make sure that you don't take more than three
minutes on this problem.
5. Prove that there is a positive integer that equals the sum of positive
integers
not exceeding it.
Solution: 3 is one such number.
6. Prove that the product of a rational number and an
irrational number is irrational.
Solution: We know that the product and quotient of two rational numbers
are also ration. Therefore, we can prove this by contradiction. Let p, q be
the two numbers with p rational and q irrational. Assume that r = pq is
rational.
Then, this implies that q = r/p is also rational, which is the desired
contradiction.
7. Prove that the proposition 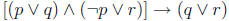 is a tautology.
is a tautology.
Solution: Compute the truth table and show that it is always true.
8. We briefly discussed the uniqueness quantifier,
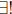 . The notation
. The notation
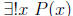
meant "There is a unique x, such that P(x) is true." Express this uniqueness
quantification 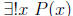 in terms of universal quantifiers, existential
quantifiers
in terms of universal quantifiers, existential
quantifiers
and logical operators. (Hint: You might need to use nested quantifiers).
Solution: Here is a partial solution:
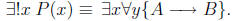
You have to figure out what to put for A and B.
9. Prove that at least one of the real numbers
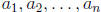 is greater
than or
is greater
than or
equal to their average.
Solution: Proof by contradiction. If all
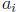 are smaller than their average,
are smaller than their average,
then you can show that this average is smaller than itself, which is the
contradiction.
10. For the following argument, explain which rules of inference are used in
each step to lead from the premises to the conclusion:
"There is someone in this class who has been to France. Everyone who
visits France visits the Louvre. Therefore, someone in this class has visited
the Louvre".
Solution: Again, the answer can be found in the textbook (Section 1.5).
11. Give one example of a trivial proof and one example of a vacuous proof.
Solution: A vacuous proof is a proof that shows the hypothesis is false.
Here is an example: Suppose x is a real number . Show that if x2 < 0, then
x2 + x6 = 2. The (vacuous) proof is to show that x2 < 0 is false if x is real
number. Then, because the hypothesis is false, the implication is always
true.
12. Use the rules of inference to prove that if
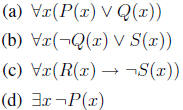
are true, then 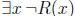 is also true.
is also true.
Solution: Work out this problem yourself. Make sure that you know how to
solve this problem. There are similar examples in the textbook and lecture
slides.
13. Prove that there cannot exist any real number x such that x2 + 1/x2 = π/2.
Solution: We did this in class.
14. If x is an integer, prove that x = floor(x/2) + ceil(x/2).
Solution: There are two cases: (1) x = 2k+1 is odd. Then floor(x/2) = k
and ceil(x/2) = k + 1. Therefore, x = floor(x/2) + ceil(x/2). Similarly,
if x is even, we can show that x = floor(x/2) + ceil(x/2).
15. Prove that 
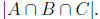
Solution: We went over this problem in class. You need to use the formula
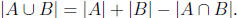
16. Give an example each of a function from the set of natural numbers to the
set of natural numbers which is (a) one-to-one but not onto, (b) onto but
not one-to-one, and (c) neither one-to-one nor onto. Prove your example in
each case.
Solution: 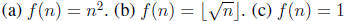 .
.
17. Let 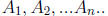 be a countable collection of countable sets. Show that
be a countable collection of countable sets. Show that
their union and intersection are also countable..
Solution: The intersection will be a subset of say
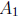 . Because
. Because 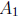 is countable,
is countable,
the intersection (which is a subset) is also countable. To show that
their union is also countable, you can do the following. First, show that
the set 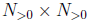 is countable, i.e., the set of cartesian product of positive
is countable, i.e., the set of cartesian product of positive
integers is countable. The required bijection is constructed exactly as in the
proof that shows the set of rational numbers is countable. Once you have
shown that 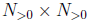 is countable, you can define an onto
function from
is countable, you can define an onto
function from
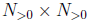 to
to 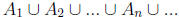 showing that the latter set is indeed
showing that the latter set is indeed
countable.
18. Determine whether each of these sets is countable. For those that are
countable,
exhibit an one-to-one correspondence between the set of natural numbers
and that set.
(a) integers not divisible by 3.
(b) integers divisible by 5 but not by 7.
(c) the real numbers with decimal representations consisting of all 1s.
(d) the real numbers with representation of all 1s or 9s.
(e) the real numbers not containing 0 in their decimal representation.
(f) the real numbers containing only a finite number of 1s in their decimal
representation.
Solution: (a) and (b) are both countable because they are subsets of the
integers.
(c) is also countable. (d) will depend on how you read the problem. If
the number can contain 1s or 9s but not both, then, it will be countable (it is
just a union of two countable sets). However, if the number can contain both
1 and 9 in its decimal representation, then, the set is uncountable. Cantor's
diagonal argument can be used here to show that this set is uncountable. (e)
and (f) are both uncountable.
19. Let f be a function from the set A to the set b. Let S and T be subsets of
A.
Show that
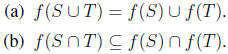
Solution: Here we show how to solve (a). Let x ∈ f(S ∪ T). This means
that there exists an y ∈ S ∪ T such that f(y) = x. If y ∈ S, then x ∈ f(S).
Else, y ∈ T, then x ∈ f(T). This shows that x ∈ f(S) ∪ f(T). Conversely,
if x ∈ f(S) ∪ f(T). If x ∈ f(T), there exists y ∈ T such that f(y) = x.
This shows that x ∈ f(S ∪ T).
20. Compute the sum 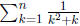 .
.
Solution: 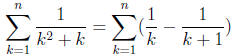
This telescoping sum is simply 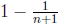 .
.
| Prev | Next |