DISTANCE,CIRCLES,AND QUADRATIC EQUATIONS
• THE GRAPH of y = ax2 + bx + c
An equation of the form
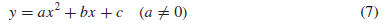
is called a quadratic equation in x. Depending on whether a is positive or
negative, the
graph, which is called a parabola, has one of the two forms shown in Figure G.7.
In both
cases the parabola is symmetric about a vertical line parallel to the y-axis.
This line of
symmetry cuts the parabola at a point called the vertex. The vertex is the low
point on the
curve if a > 0 and the high point if a < 0.
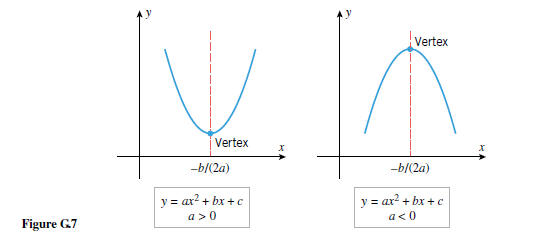
In the exercises (Exercise 78) we will help the reader show that the
x-coordinate of the
vertex is given by the formula
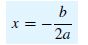
With the aid of this formula, a reasonably accurate graph of a quadratic
equation in x can
be obtained by plotting the vertex and two points on each side of it.
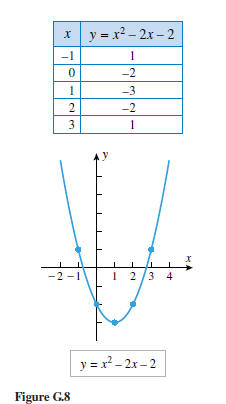
Example 9 Sketch the graph of
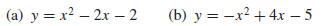
Solution (a). The equation is of form (7) with a = 1, b = −2, and c = −2, so
by (8)
the x-coordinate of the vertex is
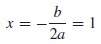
Using this value and two additional values on each side, we obtain Figure G.8.
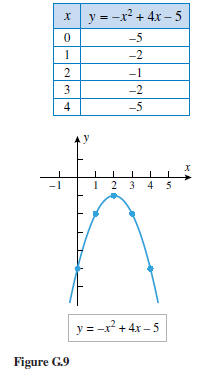
Solution (b). The equation is of form (7) with a = −1, b = 4, and c = −5, so
by (8)
the x-coordinate of the vertex is
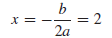
Using this value and two additional values on each side, we obtain the table
and graph in
Figure G.9.
Quite often the intercepts of a parabola y = ax2 + bx + c are important to
know.
The y-intercept, y = c, results immediately by setting x = 0. However, in order
to obtain
the x-intercepts, if any, we must set y = 0 and then solve the resulting
quadratic equation
ax2 + bx + c = 0.
Example 10 Solve the inequality
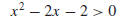
Solution. Because the left side of the inequality does not have
readily discernible factors,
the test-point method illustrated in Example 4 of Appendix A is not convenient
to use.
Instead, we will give a graphical solution. The given inequality is satisfied
for those values
of x where the graph of y = x2 − 2x − 2 is above the x-axis. From
Figure G.8 those are
the values of x to the left of the smaller intercept or to the right of the
larger intercept. To
find these intercepts we set y = 0 to obtain
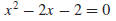
Solving by the quadratic formula gives
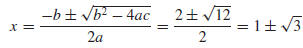
Thus, the x-intercepts are

and the solution set of the inequality is
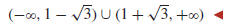
Note that the decimal approximations of the intercepts calculated in the
preceding example agree
with the graph in Figure G.8. Observe, however, that we used the exact values of
the intercepts to
express the solution. The choice of exact versus approximate values is often a
matter of judgment
that depend son the purpose for which the values are to be used. Numerical
approximations often
provide a sense of size that exact values do not, but they can introduce severe
errors if not used
with care.
Example 11 From Figure G.9 we see that the parabola y = −x2
+ 4x − 5 has no
x-intercepts. This can also be seen algebraically by solving for the
x-intercepts. Setting
y = 0 and solving the resulting equation
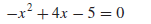
by the quadratic formula yields
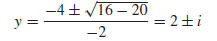
Because the solutions are not real numbers, there are no x-intercepts.
Example 12 A ball is thrown straight up from the surface of the Earth
at time t = 0 s
with an initial velocity of 24.5 m/s. If air resistance is ignored, it can be
shown that the
distance s (in meters) of the ball above the ground after t seconds is given by

(a) Graph s versus t , making the t-axis horizontal and the s-axis vertical.
(b) How high does the ball rise above the ground?
Solution (a). Equation (9) is of form (7) with a = −4.9, b = 24.5, and c = 0,
so by (8)
the t-coordinate of the vertex is
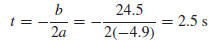
and consequently the s-coordinate of the vertex is
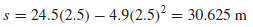
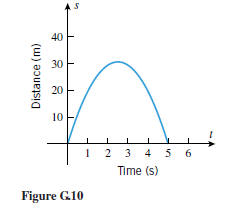
The factored form of (9) is
s = 4.9t (5 − t)
so the graph has t-intercepts t = 0 and t = 5. From the vertex and the
intercepts we obtain
the graph shown in Figure G.10.
Solution (b). From the s-coordinate of the vertex we deduce that the ball
rises 30.625 m
above the ground.
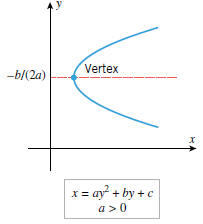
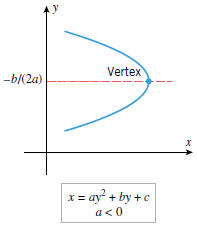
• THE GRAPH of x = ay2 + by + c
If x and y are interchanged in (7), the resulting equation,
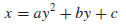
is called a quadratic equation in y. The graph of such an equation is a
parabola with its line
of symmetry parallel to the x-axis and its vertex at the point with y-coordinate
y = −b/(2a)
(Figure G.11). Some problems relating to such equations appear in the exercises.
| Prev | Next |