Division of Mathematics and Physics Project #3
This project is due 03/12/2007. Be neat, orderly , and
answer every question. Answers without
work will not receive credit.
1. A polynomial equation is given along with information about factors. Use the
information
to solve the following equation.
x4 + 5x3 - 23x2 - 87x + 140 = 0
Given that x2 + x - 20 is a factor of x4 + 5x3 - 23x2 - 87x + 140.
Work: First you'll need to use long division, and you'll find.
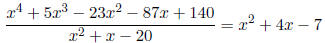
So we now have:
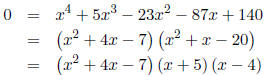
Clearly we have x = -5 and x = 4 as solutions, but we need
to use the quadratic formula
to find the zeros of x 2 + 4x - 7.
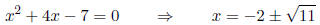
So the solution set is:
2. Find a polynomial function , of smallest degree, with
integer coefficients , that has the
following as zeros: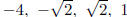 
.
Work: Using these four roots we have:
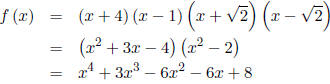
So any polynomial, where k ≠ 0 ∈ Z, of the form
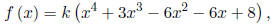
is an acceptable answer. For example, if k = 1, your answer is:
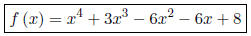
3. Given that
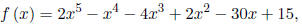
find:
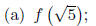
Work: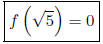 
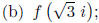
Work: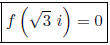 
(c) Use the above two facts to find all five roots of f .
Work: Your prior work with the quadratic formula should convince you that if
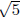
is a root then - 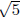is also a root; likewise if
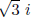is a root then -
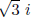is also a root.
We have one more to find.
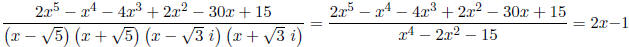
So the remaining root is 1/2.
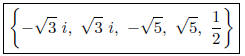
4. Use the Rational Root Theorem to factor and graph the
following function.
f (x) = x4 - 4x3 - 16x2 + 36x + 63
Work: Since it does not ask to list the candidate rational roots, I just want to nd two
reasonable ones that work.
f (-3) = 0
f (3) = 0
Now using these two roots you should realize that
(x - 3) (x + 3) = x2 - 9
is a factor of f (x), and using long division we get
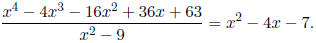
So, we have
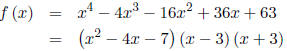
The first factor's zeros are :
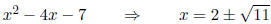
and the completely factor form of f is:
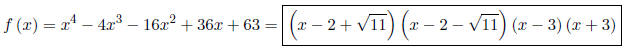
If you're graphing by hand you'll need to approximate.
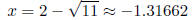and
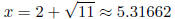
After listing all x- intercepts , the y-intercept, doing
simple sign -analysis, you should get a
graph similar to:
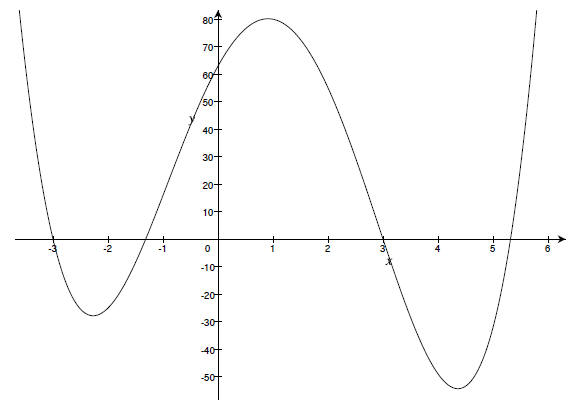
Figure 1: Partial graph of f (x) = x4 - 4x3 - 16x2 + 36x + 63.
| Prev | Next |