Inequalities

Overview
• Section 1.5 in the textbook:
– Linear Inequalities
– Compound Inequalities
– Absolute Value Inequalities
– Polynomial Inequalities
– Rational Inequalities

Linear Inequalities

Solving Inequalities
• An inequality is similar to an equality except
instead of =, we have >, <, ≤ or ≥.
– Essentially solved in the same way as an equality
• Solution set – all values that satisfy an
inequality
• Whereas an equality has at most 1 solution, the
solution to an inequality is a set – possibly with
infinitely many elements
• You will have an easier time solving inequalities
if the variable is isolated on the LEFT side

Dividing an Inequality by a
Negative
• Only point where solving an inequality
differs from solving an equality
• If the inequality is DIVIDED (or
MULTIPLIED ) by a NEGATIVE number,
SWITCH the direction of the inequality
• Adding negative numbers to both sides of
an inequality does NOT switch the
direction of the inequality!

Review of Graphing & Interval
Notation
• When graphing the solution set on a number
line:
– If the inequality is > or <, use parentheses ( )
– If the inequality is ≥ or ≤, use brackets [ ]
• Interval notation represents the “endpoints” of
the graph of the number line
– First value is what is shaded furthest to the left on
the graph
– Second value is what is shaded furthest to the right
on the graph
• A shaded arrow on the number line represents ∞
– Parentheses ALWAYS go around infinity

Solving Inequalities (Example)
Ex 1: Solve, graph, and write the solution in
interval notation:

Ex 2: Solve, graph, and write the solution in
interval notation:

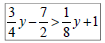
Compound Inequalities

Solving Compound Inequalities
Using Union
• Two inequalities separated by the word or
• Solve each linear inequality as normal
• To graph, draw 3 number lines with equal
intervals:
– On the first number line, graph the solution to
the first inequality
– On the second number line, graph the
solution to the second inequality
– On the third number line, lay the first two
number lines on top of each other – this
represents the union

• Determine the endpoints and remove any
parentheses or brackets that are not on the
endpoints
– Obtain the interval notation from the union
• If two areas of the number line are
shaded:
–Write the interval notation for the left part
–Write the interval notation for the right part
– Union the two intervals

Ex 3: Solve, graph, and write the solution in
interval notation:
5x + 17 ≥ 22 or 2(x – 3) + 1 < -13

Ex 4: Solve, graph, and write the solution in
interval notation:
3(x – 4) + 8 > 5 or 10x ≤ 30

Ex 5: Graph and write the solution in
interval notation:
x ≥ 2 or x > 7

Compound Inequalities Separated
by and
• Solve each linear inequality as normal
• To graph, draw 3 number lines with equal
intervals:
– On the first number line, graph the solution to
the first inequality
– On the second number line, graph the
solution to the second inequality
– On the third number line, lay the first two
number lines on top of each other
– The intersection is the area between the left
parenthesis (or [) and the right parenthesis
(or ])
• Obtain the interval notation from the intersection
– It is possible that there is no intersection

Ex 6: Solve, graph, and write the solution in
interval notation:
2(x – 3) < -9 and -2x + 7 ≤ 3x + 22

Ex 7: Solve, graph, and write the solution in
interval notation:
5(x – 2) < -10 and -9x < -18

Compound Inequalities with Two
Inequality Symbols
• Most common way to see a compound inequality
involving intersection
– Ex: -2 < x – 3 < 5
• To solve:
– Goal is to isolate the variable between the two
inequality symbols
– Perform Algebraic operations on three sides instead
of two
• Simple to graph:
– Once the variable is isolated, the intersection is
already obtained
• No need to draw three graphs

Ex 8: Solve, graph, and write the solution in
interval notation:
-12 ≤ 2 – 5x < 7

Ex 9: Solve, graph, and write the solution in
interval notation:

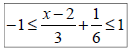
Absolute Value Inequalities

Absolute Value Inequalities
• Recall that absolute value measures distance
• If we say |x| < c, then the solution set contains all points
c units from 0 (left and right)
– Graph:

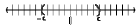
– Interval notation: (-c, c)
• If we say |x| > c, then the solution set contains all points
more than c units from 0 (left and right)
– Graph:

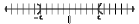
– Interval notation: (-oo, c) U (c, +oo)

Solving Absolute Value Inequalities
• The absolute value inequality can be
transformed into a compound inequality based
on the inequality sign:
– If < or ≤,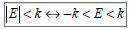
• Intersection
– If > or ≥,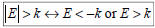
• Union

Ex 10: Solve, graph, and write the solution
in interval notation:
|3x – 2| – 2 > -1

Ex 11: Solve, graph, and write the solution in
interval notation:

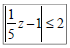
Polynomial Inequalities

Solving Polynomial Inequalities
• We discussed how to solve polynomial
equalities
• Only difference is that the solution set now
consists of intervals instead of real
numbers
• To solve an inequality such as
(x + 1)(x – 1) > 0:
– By the Zero Product Principle, x = -1 or x = 1
– This subdivides the interval (-oo, +oo) into
three subintervals:
(-oo, -1), (-1, 1), (1, +oo)

– Sign Property of polynomials : if one value
in a subinterval yields a certain sign, then
ALL values in the subinterval have that SAME
sign
• First must separate (-oo, +oo) into subintervals
by using the solutions to the polynomial
• Ex: Since x = -5 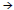24 > 0, ALL values in (-oo, -1)
are positive
– Thus, pick one value in each subinterval and
test it in the inequality
• Keep only those intervals that satisfy the inequality
• If more than one interval satisfies the inequality,
union them

Ex 12: Solve and write the solution in
interval notation:
2x² – x < 10

Ex 13: Solve and write the solution in
interval notation:
x³ + x² – 12x ≥ 0

Rational Inequalities

Solving Rational Inequalities
• Almost the same process as solving a
polynomial inequality
• Also need to consider values for the
variable that cause the denominator to
equal 0
• To solve a rational inequality:
– Set one side to ZERO and write the other side
as a rational expression
– Determine the critical values – those values
that cause either the numerator or
denominator to equal 0
– Split (-oo, +oo) into subintervals based on
the critical values
• Just as with a polynomial inequality
– Test each subinterval to determine those that
are included in the solution set
• The sign rule for polynomials applies for rational
expressions as well
– If necessary, adjust the intervals for
extraneous solutions!

Ex 14: Solve and write the solution in interval
notation:

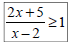
Ex 15: Solve and write the solution in interval
notation:

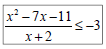
Summary
• After studying these slides, you should know how to do
the following:
– Solve, graph, and write the solution set in both interval and set
builder notation for the following types of inequalities:
• Linear
• Compound
• Absolute value
• Polynomial
• Rational
• Additional Practice
– See the list of suggested problems for 1.5
• Next lesson
– Graphing & Circles (Section 2.1)