Introduction to Number Theory
Extended Euclidean Algorithm
– algorithm steps :
– thus, we get
• Also, if gcd(a, b) = 1, then ax+by = 1, i.e., ax mod b = 1
• Input: integers a ≥ b > 0
• Output: g = gcd(a, b) and x and y with ax+by = gcd(a, b)
• The algorithm itself:
x = 1; y = 0; g = a; r = 0; x = 1; t = b
while (t > 0) {
q = [g/t]
u = x − qr; v = y − qs; w = g − qt
x = r; y = s; g = t
r = u; s = v; t = w
}
• Algorithm invariants: ax+by = g and ar +bs = t
• Complexity of the algorithm (theorem)
– this result is due to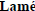 
, 1845
– the number of steps ( division operations ) needed by the Euclidean
algorithm is no more than five times of decimal digits in the smaller
of the two numbers
• Corollary
– the number of bit operations needed by the Euclidean algorithm is
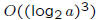, where a is the larger of the two numbers
Prime and Composite Numbers
• Prime numbers
– a prime number is an integer greater than 1 which is divisible by 1
and itself
– the first prime numbers are 2, 3, 5, 7, 11, 13, 17, etc.
• Composite numbers
– a composite number is an integer greater than 1 which is not prime
– the composite numbers are 4, 6, 8, 9, 10, 12, 14, etc.
• Relatively prime numbers
– integers a and b are relatively prime is gcd(a, b) = 1
– relatively prime numbers don’t have common divisors other than 1
Decomposition of numbers
• Fundamental Theorem of Arithmetics :
– every integer n > 1 can be written as a product of prime numbers
– and this product is unique if the primes are written in
non- decreasing order
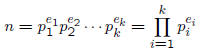
– here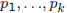 
are the primes
that divide n and 
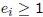is the
number of factors of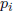 
dividing n
– this decomposition is called the standard representation
• Example: 84 = 2 · 2 · 3 · 7 = 22 · 31 · 71
Using Standard Representation
• GCD and LCM
– we are given n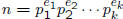
and
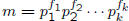, where pi
are prime numbers and
– 
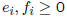
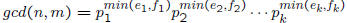
– the least common multiple of integers a and b is the smaller positive
integer divisible by both a and b
–
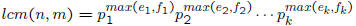
– also, gcd(a, b) · lcm(a, b) = ab
• Examples:
– n = 84 = 22 · 3 · 7
– m = 63 = 32 · 7
– gcd(84, 63) =
– lcm(84, 63) =
– gcd(84, 63) · lcm(84, 63) =
Distribution Distribution of prime numbers
• In cryptography, we’ll need to use large primes and
would like to know
how prime numbers are distributed
• (Theorem) The number of prime numbers is infinite
• (Theorem) Gaps between primes
– for every positive integer n, there are n or more consecutive
composite numbers
• For a positive real number x, let π(x) be the number of prime numbers
≤
x
• The Prime Number Theorem
– π(x) tends to x/ ln x as x goes to infinity. In symbols ,
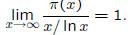
– this tells us that there are plenty of large primes
• The question now is how we find prime numbers
• Theorem
– if integer n > 1 is composite, it has a prime divisor
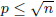
– in other words, if n > 1 has no prime divisor
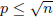, then it is
prime
Finding Primes
• This suggests a simple algorithm for testing a small
number for
primality (and factoring if it is composite)
– Input: a positive integer n
– Output: whether n is prime, or one or more factors of n
m = n; p = 2
while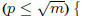 
if (m mod p = 0) {
print “n is composite with factor p”; m = m/p
}
else { p = p+1 }
}
if (m = n) { print “n is prime” }
else if (m > 1) { print “the last factor of n is m”}
• Today we’ve learned:
– divisibility theorems
– how to use Euclidean algorithm to compute GCD and more
– the number of prime numbers is large and they are well distributed
• More on number theory is still ahead
| Prev | Next |