Inverse Functions
Due Homework
8 webwork problems (1 hint)
Undue Homework
Textbook 2.5: 7, 9, 53, 55
Overview
• Invertability.
• Definition of an Inverse Function.
• Expressions and Inverses .
• Basic Inverses Examples.
• Graphs and Inverses .
• The Horizontal Line Test .
• Graphin an Inverse.
• Machines and Inverses.
Invertability
In section 2.1, we determined whether a relation was a function by looking for
duplicate x- values .
Invertability is the opposite. A function is invertible if and only if it
contains no two ordered
pairs with the same y-values, but different x -values. Thus, to determine if a
function is invertible, we look for duplicate y-values. Invertible functions are
also called one-to-one.
Example
Which functions are invertible?

Solution
f is not invertible since it contains both (3, 3) and (6, 3).
g is invertible.
h is invertible.
Definition of an Inverse Function
If f is an invertible function, its inverse, denoted f–1
, is the set of ordered pairs (y, x) such
that (x, y) is in f. That is, f–1 is f with its x- and y-values swapped. f–1(x)
is not
1/f(x).
Example
Find the inverses of the invertible functions from the last example.
Solution
g–1 = {(2, 1), (3, 2), (5, 4)}
h–1 = {(7, 3), (4, 4), (3, 7)}
Note
1. Invertability insures that the a function’s inverse is a function.
2. A function can be its own inverse. Observe how the function h in the last
example has this
property .
3. Whenever g is f’s inverse then f is g’s inverse also.
4. Inversion swaps domain with range. That is
dom f = ran f-1
ran f = dom
Expressions and Inverses
Example
Describe in words what the function f(x) = x does to its input.
Solution
Nothing.
The Cancellation Theorem
Functions f are g are inverses of each other if and only if both of the
following cancellation laws
hold:
(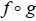 )(x) = x for all x in dom g
)(x) = x for all x in dom g
(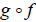 )(x) = x for all x in dom f
)(x) = x for all x in dom f
In other words, the machines 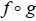 and
and
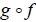 do nothing to their inputs. This means that
f reverses
do nothing to their inputs. This means that
f reverses
all changes made by g and vise versa. In essence, f and g cancel each other out.
Example
Verify that the following pairs are inverses of each other.
a) 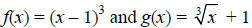
b) 
c) 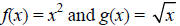
Solution
a)
b)
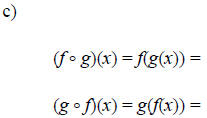
Example
If f(–7) = 8, and f is invertible, solve 1/2 f (x – 9) = 4.
Solution
1/2 f(x – 9) = 4
f(x – 9) = 8
f-1(f(x – 9)) = f-1(8)
x – 9 = –7
x = 2
Let f and g be inverses of each other, and let f(x) = y. Then by the
Cancellation
Theorem
g(y) = g(f(x)) = x
This partly proves the next theorem.
Change of Form Theorem
Functions f and g are inverses of each other if and only if both of the
following change of form
laws holds :
f(x) = y implies g(y) = x
g(x) = y implies f(y) = x
Change of Form Theorem (alternate version)
If f is invertible then
f(x) = y if and only if f–1(y) = x
Example
If f(4) = 3, f(3) = 2, and f is invertible, find f–1(3) and (f(3))–1.
Solution
f–1(3) = 4
(f(3))–1 = 2–1 = 1/2
To find the inverse of a function, f, algebraically
1. Set y = f(x).
2. Swap x with y.
3. Solve for y.
4. Replace y with f-1(x).
Example
Find the inverses of
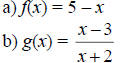
Solution
a)
y = 5 – x
x = 5 – y
x + y = 5
y = 5 – x
f–1(x) = 5 – x
Notice that f is its own inverse.
b)
Basic Inverses Examples
| f(x) | |||||||
| f–1(x) | |||||||
| Applies When |
Graphs and Inverses
To find f–1(a) from the graph of f, start by finding a on the y-axis
and move horizontally until
you hit the graph. The answer is the x- value of the point you hit.
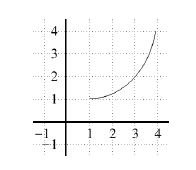
Example
Use the graph of f to find f–1(2) and f–1(3).
Solution
f–1(2) = 3
f–1(3) = 3.6
The Horizontal Line Test
The graph of a function is that of an invertible function if and only if every
horizontal line
passes through no or exactly one point.
Example
Which graph is that of an invertible function?
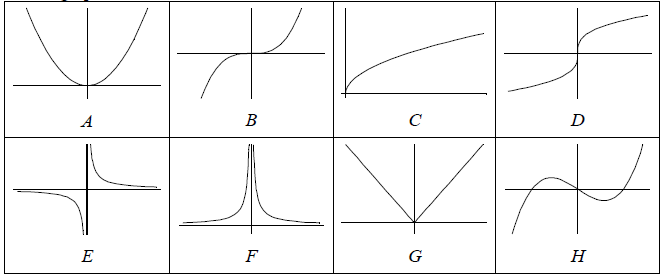
Solution
B, C, D, and E
Graphing an Inverse
To graph f–1 given the graph of f, we place a point (b, a) on the
graph of f–1 for
every point (a, b) on the graph of f. This has the effect of reflecting the
graph of f across the line y = x.
Example
a) Which pair of functions in the last example are inverses of each other?
b) Which function is its own inverse?
c) Which function is invertible but its inverse is not one of those shown?
Solution
B and Dare inverses of each other.
Eis its own inverse.
C is invertible, but its inverse is not shown
To graph f–1 given the graph of f, do the
following
1. Label several points (a, b) on f that
define its general shape.
2. For each, plot (b, a).
3. Draw the line y = x.
4. Connect the dots paying attention to the way
the graph is being reflected across y = x.
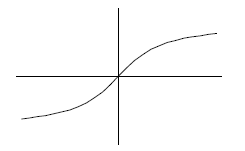
Example
Graph the inverse of the function, k graphed to
the right.
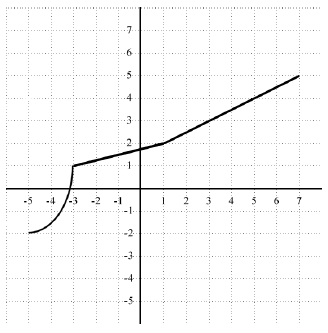
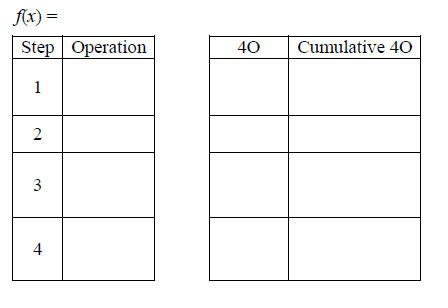
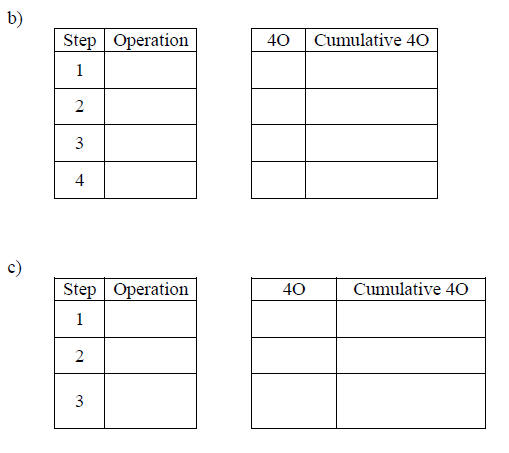
Machines and Inverses
From a machine perspective, a function f is invertible if and only if it is a
composition of
invertible operations (CIO). In this case, f-1 is the machine that performs the
opposite
operations in the opposite order (4O). When a function is a CIO, the machine
metaphor
is a quick and easy way to find its inverse. I will teach you how to do it using
a machine table, and
I may require you to show a machine table because otherwise there is no work to
show. However, that is the
point. With some practice, you can use this method to find inverses in your
head.
Example
Make a machine table for each function. If it is invertible find its inverse
using the machine table.
a) f(x) =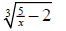
b) g(x) = 
c) h(x) =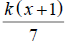 where k is the function graphed to
the right.
where k is the function graphed to
the right.
Solution
a)
| Prev | Next |