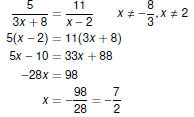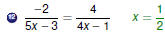Today’s Homework Assignment
| Section |
Problems |
 |
 |
|
Outline
 Complex Numbers Complex Numbers
 Definitions Definitions
 Complex Addition and Multiplication Complex Addition and Multiplication
 Complex Division Complex Division
 Extending the Square Root Extending the Square Root
 Linear Equations Linear Equations
 Definition Definition
 Manipulating Linear Equations Manipulating Linear Equations
 Problem Solving Problem Solving
 More Equations More Equations
 Variable Denominators Variable Denominators
 Ratio and Proportion Ratio and Proportion
 More Problem Solving More Problem Solving |
| Definitions
Definitions
Definition (The Imaginary Unit)
The imaginary unit i is a number such that i2 = −1. |
Definition (Complex Numbers)
A complex number is any number that can be written in the form
a + bi,
where a and b are real numbers. |
A complex number written as a +bi is said to be in
standard form.
a is called the real part of the complex number
b is called the imaginary part of the complex number |
Definitions Examples of Complex Numbers
 3 + 5i Already in standard form 3 + 5i Already in standard form
 10 − 4i 10 + (−4)i
10 − 4i 10 + (−4)i
 7 7 + 0i
7 7 + 0i
 3i 0 + 3i
3i 0 + 3i
All real numbers are |
| Complex Addition and Multiplication
Complex Addition and Multiplication
To add complex numbers, just add the real parts and
the imaginary
parts separately.
Definition
(a + bi) + (c + di) = (a + c) + (b + d)i |
To multiply complex numbers, treat them like
binomials and FOIL
the product .
Definition
(a + bi)(c + di) = (ac − bd) + (ad + bc)i |
|
Complex Division The Conjugate
Recall
the special pattern
(a + b)(a − b) = a2 − b2.
Apply this to complex numbers (replace b with bi):
(a + bi)(a − bi) = a2 − (bi)2 = a2 − b2i2 = a2 + b2.
Changing the sign of the imaginary part is a useful operation: it
can be used to produce a real number!
Definition
The conjugate of a + bi is a − bi. |
Note that a + bi is also the conjugate of a − bi. |
| Complex Division Dividing by Complex Numbers
To divide by a complex number—that is, when a fraction has a
complex denominator—use the conjugate to transform the
denominator to a real number.
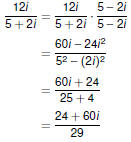 |
Examples Examples
 |
| Extending the Square Root
A Better Definition
Our definition of i (”a number such that i2 = −1”) doesn’t really
define i. It just states a property of i.
We can make the definition more specific by stating that i will be
the principal square root of −1:
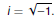
Definition
The principal square root of −b is denoted by
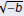 and defined and defined
as
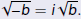 |
Now we can define square roots of negative numbers :
|
Extending the Square Root
Complications
Recall the Properties of Radicals :
These do not apply if b or c is negative! |
| Extending the Square Root
For instance, using the definition of
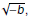 we have we have
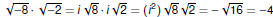
But, if we tried to use the Properties, we’d get
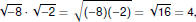
which is wrong. |
Definition Linear Equations
Definition
A linear equation in the variable x is an equation that can be
written in the form ax + b = 0. |
Examples
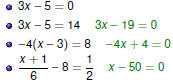
|
| Manipulating Linear Equations
Solving Linear Equations
We may add, subtract, multiply, or divide by the same quantity on
both sides of an equation. The goal is to isolate the variable by
moving everything else to the other side.
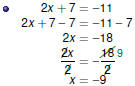
It might be necessary to simplify first .
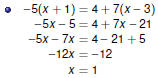
|
The Most Important Step
Always check your answers! |
Examples Part 1
Examples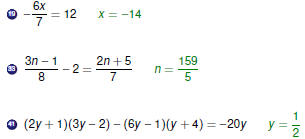
|
Problem Solving
Problem-Solving Example
 Find three
consecutive integers whose sum is 21. Find three
consecutive integers whose sum is 21.
We need to represent the three integers with variables. Call the
smallest one n. Then the other two are n + 1 and n + 2.
They add up to 21:
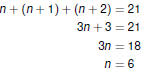
Make sure you answer the question!
The three integers are 6, 7, and 8. |
Examples Part 2
Examples
 One number is 5 less than
another number. Find the numbers One number is 5 less than
another number. Find the numbers
if five times the smaller number is 11 less than four times the
larger number. 9 and 14
 The average of the salaries of Kelly, Renee, and Nina is The average of the salaries of Kelly, Renee, and Nina is
$20,000 a year. If Kelly earns $4000 less than Renee, and
Nine’s salary is two-thirds of Renee’s salary, find the salary of
each person. $24,000 for Renee, $20,000 for Kelly,
$16,000 for Nina |
Variable Denominators
Beware of Zero Denominators !
If a variable appears in a denominator,
 multiply by a common denominator to clear fractions, and
multiply by a common denominator to clear fractions, and
 take special care to ensure that the denominator is not zero.
take special care to ensure that the denominator is not zero.
In other words, check your answers!
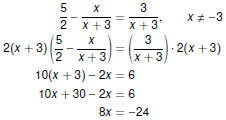
 Oops! Oops!
This equation has no solution!
|
Examples Part 1
Examples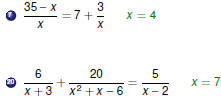
|
Ratio and Proportion
Cross-Multiplication
If both sides of an equation are single fractions, use
cross-multiplication:
The Cross-Multiplication Property
If b ≠0, d ≠ 0, and 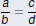 , then
ad = bc. , then
ad = bc. |
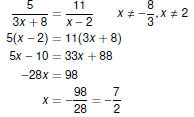
|
Examples Part 2
Examples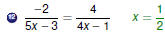
|
More Problem Solving
Examples
 One number is 100 larger than another number. If the larger One number is 100 larger than another number. If the larger
number is divided by the smaller, the quotient is 15 and the
remainder is 2. Find the numbers. 7 and 107
 A sum of $2250 is to be divided between two people in the A sum of $2250 is to be divided between two people in the
ratio of 2 to 3. How much does each person receive?
$900 and $1350
 Derek has some nickels and dimes worth $3.60. The number Derek has some nickels and dimes worth $3.60. The number
of dimes is one more than twice the number of nickels. How
many nickels and dimes does he have? 14 nickels and 29
dimes
 The length of a rectangle is 2 inches less than three times its The length of a rectangle is 2 inches less than three times its
width. If the perimeter of the rectangle is 108 inches, find its
length and width. 14 inches by 40 inches |
 One number is 100 larger than another number. If the larger
One number is 100 larger than another number. If the larger A sum of $2250 is to be divided between two people in the
A sum of $2250 is to be divided between two people in the Derek has some nickels and dimes worth $3.60. The number
Derek has some nickels and dimes worth $3.60. The number The length of a rectangle is 2 inches less than three times its
The length of a rectangle is 2 inches less than three times its
 Complex Numbers
Complex Numbers Definitions
Definitions
 More Equations
More Equations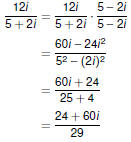

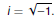
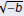 and defined
and defined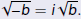
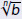 and
and
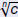 are real numbers, then
are real numbers, then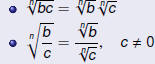
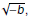 we have
we have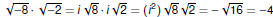
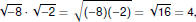
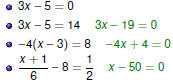
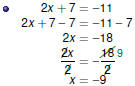
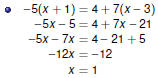
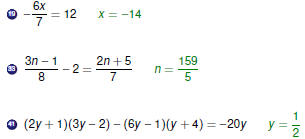
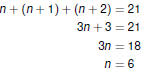
 One number is 5 less than
another number. Find the numbers
One number is 5 less than
another number. Find the numbers The average of the salaries of Kelly, Renee, and Nina is
The average of the salaries of Kelly, Renee, and Nina is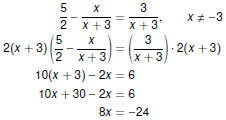
 Oops!
Oops!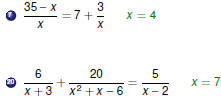
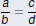 , then
ad = bc.
, then
ad = bc.