Math 0824.003 FINAL REVIEW
1. In the county of Philadelphia the number of existing home sales in 2007 was 1,254 and in 2008 it was 969. Determine the percent of change in sales of existing homes. (Give your answer to the nearest tenth of a percent.)
2. The population of Scooterville is increasing at a rate of 351 people per year. If the population is 354 today, what will it be in three years? Determine whether the growth (or decay) is linear or exponential .
3. The population of Oak Forest is increasing at a rate of 3% per year. If the population is 64,792 today, what will it be in three years? Determine whether the growth (or decay) is linear or exponential.
4. The doubling time of a population of bacteria is 2 hours. By what factor does the population increase in 10 hours?
5. The Consumer Price Index is increasing at a rate of 7% per year. What is its doubling time? (Give your answer to the nearest whole year.)
6. Frank's Furniture employees earned the displayed amounts last week. Determine the mean amount earned by employees last week. (Give your answer to the nearest whole dollar.)
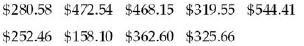
7. The salaries of ten randomly selected doctors are displayed. Determine the median salary. (Give your answer to the nearest whole dollar.)
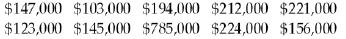
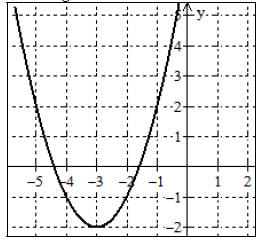
8. Determine the equation of the parabola shown
in the figure below.
9. The graph of y = ax2 + bx +c is shown
to the right. Use it to respond to the
following.
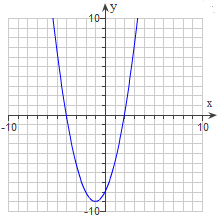
(i) Circle the correct answer:
a > 0 a < 0
(ii) Solve ax 2 + bx +c = 0. Circle the
correct choice.
x = -2, 4
x = 2, -5
x = 2, -4
(iii) What is the discriminant of ax2 + bx +c = 0? Circle the correct choice.
Positive Negative Zero
10. A carpenter is building a rectangular room with a
fixed perimeter of 216 ft. What dimensions would yield the maximum area? What is
the maximum area?
Length = _________ ft. Width = __________ft. Maximum area = _____________sq. ft.
11. A rocket is fired upward from some initial height above the ground. Its height h in feet above the ground t seconds after it is fired is given by h = -16t2 + 48t +448.
(i) What is its initial height? __________ ft.
(ii) What is its maximum height?
___________ ft.
(iii) How long does it take to reach the ground? __________ sec.
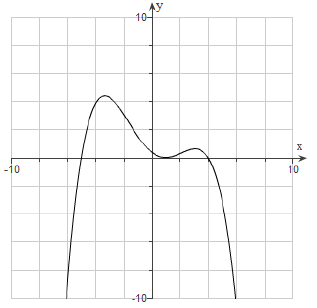
12. The figure displays the graph of a polynomial y = f(x). Use it to answer the following.
(i) List all the x-intercepts: _______________________
(ii) Is the leading coefficient positive or negative? Circle your choice.
Positive Negative
(iii) What is the minimum degree of f? _____________
13. Find all solutions of sqrt(14x-6)=x+3. (If there are no
solutions, write NONE.)
x = __________________
14. Let
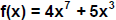 .
Circle the correct choice: ODD function EVEN function NEITHER
.
Circle the correct choice: ODD function EVEN function NEITHER
15. Write a polynomial f(x) in completely factored form,
with leading coefficient 1 that satisfies the following conditions.
Degree 4; zeros at , -3 with multiplicity 2, 2, and 4.
Also sketch a possible graph of f(x). =>
16. Meteorologists can determine the duration of a storm
using the formula T(D)=0.07D3/2where D is the diameter of the storm in miles
and T is the time in hours.
(i) If D = 10, determine the duration of the storm.
T = ______________ hours
(Give your answer to the nearest tenth of an hour.)
(ii) If the storm lasts 15 hours determine the diameter D of the storm.
D = ______________ miles
(Give your answer to the nearest tenth of a mile.)
17. In the triple crown of horse racing the Preakness (held at the Pimlico race
track in Maryland) is the shortest with a distance of
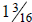 1miles. Horse racing
followers often give the length of a race in furlongs; 1 furlong = 0.125 miles.
Determine the length of the Preakness in furlongs; Length = __________ furlongs
(Give your answer to the nearest tenth.)
1miles. Horse racing
followers often give the length of a race in furlongs; 1 furlong = 0.125 miles.
Determine the length of the Preakness in furlongs; Length = __________ furlongs
(Give your answer to the nearest tenth.)
18. Suppose that $20,000 is invested at 5% interest.
(i) If interest compounded annually , what is the amount of money after 3 years?
Amount = __________ (Give your answer to the nearest cent.)
(ii) If interest compounded continuously, what is the amount of money after 3
years?
Amount = __________ (Give your answer to the nearest cent.)
19. Find the doubling time t of an investment earning 6% interest if interest is
compounded continuously.
t = ___________ years (Give your answer to the nearest tenth.)
20. Let 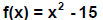 and
and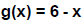 .
Determine each of the following compositions.
.
Determine each of the following compositions.
(i) (fog)(x)=__________________
(ii) (fof)(x)=_________________
(iii) (gסf)(4)=______________
21. Write the letter of the correct graph for y = 3x on the line provided. Answer: _________
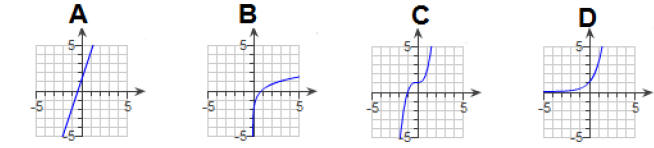
22. Find C and a so that f(x) = Cax satisfies the given
conditions. f(0) = 17, f(3) = 68.
(i) C = ___________ (Give all answers to the nearest tenth.)
(ii) a = ___________
23. The population of a country is shown in the table. A
logistics model 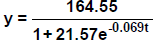 is
is
constructed where t is the number of years since 1900.
| Year | 1900 | 1920 | 1940 | 1960 | 1980 | 2000 |
| Population In millions |
7 | 26 | 70 | 123 | 152 | 161 |
(i) Estimate the population in year 2010.
Answer: ___________ millions (Give your answer to the nearest million.)
(ii) On the axes given sketch the shape of the graph of the logistics model.
24. Find the equation of either a linear or exponential
function that models the data in the table.
Answer: f(x) = _______________
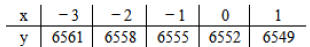
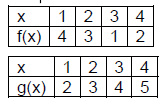
25. Functions f(x) and g(x) are given in the tables
displayed.
Compute the following if possible
26. We have points P(-1,5) and Q(-8,-1). Determine each of
the following.
(i) Find the midpoint of line segment PQ. Midpoint: ______________
(ii) Find the length of line segment PQ. Length = _______________
(iii) Find the equation of the line through P and Q. Equation:
_____________________
27. A person is driving a car on a straight road. The graph shows the distance y in miles that the individual is from home after x hours.
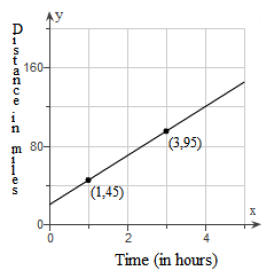
(i) Determine the equation of the line in slope-intercept form.
Equation: __________________________
(ii) How fast is the car traveling? _________ miles per hour
(iii) How far was the individual from home initially? ___________miles
(iv) How far was the individual from home after 3 hours and fifteen minutes?
________________ miles
28. In your math course there are five exams, each worth
100 points. You have scores of 89, 85, and 83 on the first three exams. You must
have a total in all the exams of 410 in order to get a B. What is the average
score you need on each of the last two exams in order to get the B?
Average score needed = _____________
29. A regression line will go through a point whose x- coordinate is the mean of the x- values and y -coordinate is the mean of the y-values. Use the data in the table to determine which of the following equations is the regression line for the data. Circle the correct choice.
| x | 50 | 60 | 70 | 80 | 90 |
| y | 165 | 166 | 169 | 171 | 174 |
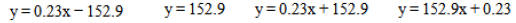
30. Let 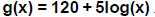 . Compute
. Compute
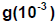 . Answer: _______________
. Answer: _______________
31. Solve for x.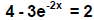 x = ________ (Give your answer to the nearest thousandth.)
x = ________ (Give your answer to the nearest thousandth.)
32. The population P of a city was 250 thousand in 1998. The population was
decreasing by 1.2% per year. Determine the population 5 years later. (Use time t
= 0 for 1998.)
Population = ____________ thousand (Give your answer to the nearest tenth.)
33. An object is placed in a freezer. Its temperature A in °F after t minutes is
given by 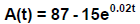 .
.
(i) Find the object’s initial temperature. Initial temperature = _______ °F
(ii) Find the temperature after 25 minutes. Temperature = ________ °F
(iii) Determine the time t when the temperature reaches 50°F. Time = _________
minutes
(Give all answers in whole numbers.)
34. Determine the area of the triangle with vertices A(-3,2), B(1,6), and
C(8,-2). Area = ___________ sq. units
(Give your answer to the nearest tenth.)
35. Determine the area of the quadrilateral ABCD where A(-4,3), B(3,6), C(1,2),
and D(5,-5). It may be helpful to sketch the figure. (Give your answer to the
nearest tenth.)
Area = _____________ sq. units
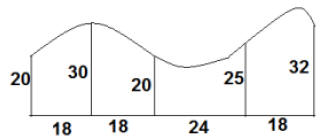
36. Use the Trapezoidal Rule to approximate the area of the figure below. All dimensions are in yards. Answer: _______
37. Sketch the inverse of f(x) and g(x) on the figure below.
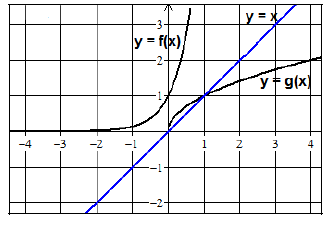
38. Compute the average rate of change for
g(x) = 2x2 - 4x between x1 = 1 and x2 = 4.
Answer = _________
39. The minimum cost for a construction of a deck is
modeled by a quadratic function with vertex at (50, 30)
and it is known that when x = 65, y = 45. Find the
quadratic equation. Answer: _____________________
40. The height of a tree in feet after x years is modeled
by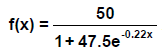
What appears to be the maximum height of the tree? Answer: ____________
For each statement determine if it is true or false.
1. On a linear function, it does not matter which two distinct points on the
line you use to calculate the slope.
2. The graph of every linear function crosses the horizontal axes exactly once.
3. If the slope of a linear function is negative then the rate of change along
the line steadily decreases.
4. -82 = (-8)2
5. bm•bm = bm^2
6. If10x = 36, then. x≈1.556.
7. l og(-5) = -log(5)
8. e2x = (ex)2
9. The graph of 6 y = 6•2x is decreasing.
10. The rate of change between any two points on the graph of y=32.5(1.06)x is
always the same.
11. If y =100(0.976)x, then when x increases by 1, y decreases by 97.6%.
12. Increasing $1000 by $100 per year for 10 years gives you more than
increasing $1000 by 10% per year for 10 years.
13. All exponential functions are increasing.
14. Quantities that increase by a constant amount represent linear growth,
whereas quantities that increase by a constant percent represent exponential
growth.
15. ln(a) = b, means eb = a.
Answer the following.
1. Describe in words the following functions by identifying the type of
function, the initial value, and what happens when x is increased by 1 unit.
(i) (fx) = 100(1.08)x
(ii) (gx) = 100 - 4x
(iii) h(x) = 25(0.85)x
2. Give an example of a number x so that log(x) lies between 2 and 3.
3. Describe the graph of power function y=1/x.
4. Give and example of a function whose domain is just all real positive real
numbers.
5. Give the equation of a quadratic function that has vertex (-1,4) and goes
through the point (0, 2).
6. Given an example of a polynomial whose graph does not intersect the
horizontal axis.
7. Describe the graph of a quadratic whose discriminant is zero.
8. Give an example of a function that has no inverse.
9. What does it mean to say that a function is one-to-one?
10. Describe the graph of a logistic function.
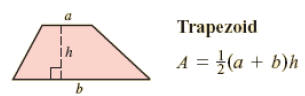
Some Formulas:

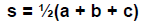
and then the area of triangle T is computed from the
expression
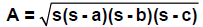
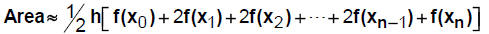
| Prev | Next |