Math Test 2B Solutions
C. HECKMAN TEST 2B
SOLUTIONS 170
(1) [10 points] For the rational function below, find its
x-intercept(s), y-intercept(s), vertical
asymptotes, horizontal asymptotes, and determine whether it is even, odd, or
neither. (If the function does not have any vertical asymptotes (for example),
make
sure you answer “none”; do not leave your answer blank.)
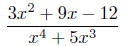
Solution: Its x-intercept is where y = 0, or when
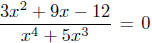 , which is
, which is
when the numerator is zero . The numerator factors into 3(x + 4)(x − 1), so the
x-intercepts are −4 and 1 .
The y-intercepts are where x = 0. If you substitute x = 0 into the formula,
you have to divide by zero , so this function has no y-intercept .
The vertical asymptotes occur where the denominator is zero but the numerator
isn’t. Since the denominator is zero when x3(x + 5) = 0, the vertical
asymptotes are x = 0 and x = −5 .
To find the horizontal asymptote, we look at the degrees of the numerator
and denominator. Since the degree of the denominator is greater, there is a
horizontal asymptote of y = 0 .
Since 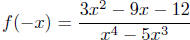 , which is neither the original
function nor its
, which is neither the original
function nor its
negative , this function is neither even or odd.
Grading: +2 points for each answer. Partial credit: +1 point for each answer.
Do the following for the equation 2y = 5:
(a) [5 points] Convert it into logarithmic form .
Solution: 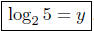 .
.
Grading for partial credit: +2 points total for taking logarithms of both sides.
(b) [10 points] Solve for y , rounding your answer to three decimal places .
Solution: You can take logarithms of both sides here, and solve for y, or use
the
change of basis formula:
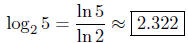
Note that 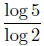 will also
give you the correct answer.
will also
give you the correct answer.
(3) Solve the following equations for x . You must give exact answers!
(a) [10 points] ln(x + 1) + ln(2x − 1) = 3
Solution: Since there are multiple logarithms , you need to combine them :
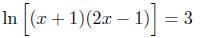
Now convert to exponential form :
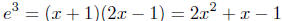
so you need to solve the quadratic equation
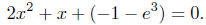
[You got 4 points for getting this far.] The solutions to
this quadratic equation
are 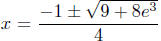 [7 points], but only the solution with
the + sign makes
[7 points], but only the solution with
the + sign makes
the original equation true. So the only solution is
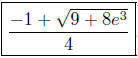 . (This is not
. (This is not
3, since e3 is not exactly 20 but only approximately 20.)
Grading for partial credit: +3 points for miscellaneous work.
(b) [10 points] 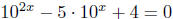
Solution: If you let y = 10x, you find out that
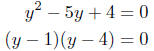
[3 points] so y = 1 or y = 4 [7 points]. To find x, you
solve the equations 10x = 1
(which has a solution of 0) and 10x = 4 (which has a solution of log 4). Both
solutions work in the original equation, so the solutions are 0 and log 4
.
Grading for partial credit: +7 points for 4 and 1. Points were taken off for
an approximate answer.
(4) A bank offers a savings account where the interest is compounded 5.1%
quarterly.
(a) [5 points] If you deposit $300 now, how much money will you have in 4 years?
Solution: Use the compound interest formula:
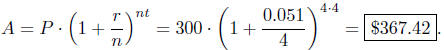
Grading: +2 points for the formula, +2 points for
substituting, +1 point for
the final answer. Grading for partial credit: −2 points for
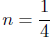 .
.
(b) [10 points] When will you have $400 in your account?
Solution: You need to solve the equation
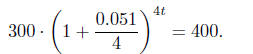 [3 points]
[3 points]
To solve this equation, you have to start by dividing both sides by 300; the
left-hand side is not 303.8254t.
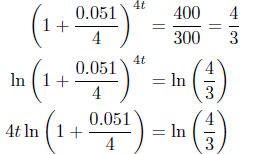 [7 points]
[7 points]
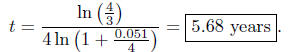 [10 points]
[10 points]
Grading for partial credit: −3 points for not dividing by 300 first.
(5) [10 points] Find a polynomial p (x) which has degree 4,
has 2 as a root, has −1 as a
root of multiplicity 3, and where p(1) = −24.
Solution: Since you know information about the roots (zeros), it is best to work
with the factored form. Since −1 has multiplicity 3, (x + 1)3 is a
factor of p(x),
and (x−2) is also a factor of p(x). Note that if the multiplicity of 2 were
greater
than 1, then p(x) would have degree at least 5. Hence p(x) = A(x − 2)(x + 1)3
for some constant A.
If you use the condition p(1) = −24, you find out that
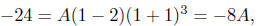
so A = 3. Thus 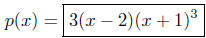 .
.
Grading for partial credit: +3 points (total) for involving (x − 2)(x + 1);
+7 points (total) for (x − 2)(x + 1)3.
(6) [10 points] Find the quotient and remainder when
3x4−7x2+8x+5 is divided by x2+2.
Solution: Since the divisor is not of the form x − c, you must use long
division:
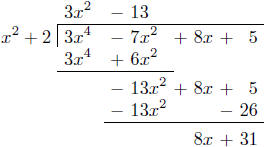
The quotient is 3x2 − 13 , and the remainder is 8x + 31 .
Grading was done on a 0–3–5–7–10 point basis.
(7) [10 points] Using the Rational Root Theorem, list the
possible rational roots of the
polynomial 3x4 −8x2 +5x−4. You do not need to determine which are actual roots.
Solution: The Rational Root Theorem states that all rational roots of this
polynomial
are of the form 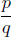 , where p is a factor of −4,
and q is a factor of 3. Since
, where p is a factor of −4,
and q is a factor of 3. Since
the factors of −4 are 1, 2, 4, −1, −2, and −4, and the factors of 3 are 1, 3,
−1,
and −3, we take all possible combinations to get the list below.
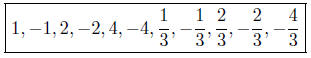
Grading: +3 points for the factors of −4, +3 points for
the factors of 3, and
+4 points for combining them. Grading for common mistakes: +8 points (total)
if the reciprocals were given.
(8) [10 points] The rational roots of the polynomial
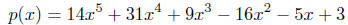
are −1 and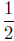 . Find all
roots of p(x) exactly, along with their multiplicities.
. Find all
roots of p(x) exactly, along with their multiplicities.
Solution: First of all, you should divide p(x) by x − (−1), and then divide that
quotient by 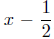 , to try to find an equation that
the other roots must satisfy.
, to try to find an equation that
the other roots must satisfy.
Doing this division (by long division or synthetic division) yields f(x) =
14x3 + 24x2 + 4x − 6.
You can’t use the quadratic formula on f (x), since f(x) has degree three.
The instruction to find the multiplicities suggests that −1 or
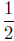 may have multiplicity
may have multiplicity
greater than one, so you should divide f(x) by x+1 and 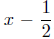 again, to see
again, to see
whether one of these divisions produces a remainder of 0. In fact, x + 1 divides
into f(x) without a remainder. The quotient of this final division is
14x2+10x−6,
and we can use the quadratic formula to find the remaining roots: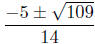 .
.
The roots of p(x) are thus −1 (with multiplicity 2, since you divided by x+1
twice), 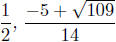 , and
, and
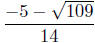 .
.
Grading: +5 points for finding f(x), +2 points for dividing again by x + 1,
+3 points for using the quadratic formula. Grading for partial credit: +5 points
(total) for −1 and 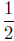 .
.
| Prev | Next |