Mathematics 12A Algebra Level I

About the Author

Rebecca Alano knew at the age of 10 that she wanted to be a teacher. It
wasn’t until she took algebra in high school that she realized what subject she
wanted to teach. “When I was introduced to the logical , beautiful language of
mathematics through algebra, I was hooked.” Mrs. Alano thoroughly enjoys
studying mathematics and sharing her love of the subject through teaching others
about it. From 1994 to 2001, she taught nine different Independent Study Program
math courses—all nine of them at once for a short period of time. “It was a great
way for me to stay at home with my children and still be actively teaching math
to students all over the world.” Once her children started school, she because a
full-time copy editor for the instructional development unit of the School of
Continuing Studies, where she helps create the learning guides that accompany
independent study courses. “Writing the learning guide for an independent study
course forces me to develop creative ways of explaining concepts to students. I’m
still teaching—just not in as direct a fashion.” When not working as a copy editor,
Mrs. Alano enjoys reading mysteries, cross-stitching, working in her church,
attending plays and concerts with her husband, and reading Harry Potter books
with her two children.

Table of Contents: Mathematics 12A

Important Information . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . i
Study Hints . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . iii
Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . v
Study Materials Order Form

Lessons

1 Slopes and Equations of Lines . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
2 Graphing Lines and Linear Inequalities; Exponents . . . . . . . . . . . . 25
3 Power Rules and Graphing Quadratic Equations . . . . . . . . . . . . . . . 51
4 Tips for the First Examination . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81
Application for the First Examination
5 Solving Quadratic Equations; Square Roots ; Polynomials . . . . . . . 91
6 Linear Systems . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 133
7 Tips for the Second Examination . . . . . . . . . . . . . . . . . . . . . . . . . . . 167
Application for the Second Examination
8 Factoring . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 175
9 Functions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 213
10 Tips for the Final Examination . . . . . . . . . . . . . . . . . . . . . . . . . . . . 241
Application for the Final Examination
11 Cumulative Project Evaluation . . . . . . . . . . . . . . . . . . . . . . . . . . . . 249
Bulletin Request Form
Selling Your Textbooks
Appendix A: Answers to the Practice Problems and
Practice Exams . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 251

Appendix B: Skill Enhancement Exercises
 The Slope of a Line . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 325
  Products and Powers of Powers . . . . . . . . . . . . . . . . . . . . . . 325
 Negative Exponents . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 326
 Quotients of Powers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 326
 Powers of Products and Quotients . . . . . . . . . . . . . . . . . . . . 327
 Using the Quadratic Formula . . . . . . . . . . . . . . . . . . . . . . . . 327
 Multiplying Polynomials . . . . . . . . . . . . . . . . . . . . . . . . . . . 328
 Solving Systems of Equations . . . . . . . . . . . . . . . . . . . . . . . 329
  Factoring x ^2 + bx + c . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 330
 Factoring ax^2 + bx + c . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 331

Appendix C: Answers to Skill Enhancement Exercises . . . . . . . . . 333
Appendix D: Instructions for Using GCalc . . . . . . . . . . . . . . . . . . . 341

Introduction

Welcome to the second semester of algebra• You’re continuing your study of
a very exciting topic. The word algebra comes from the Arabic al-jabr, which
means “the reunion of broken parts.” I like to view algebra as a puzzle having
many pieces that can be put together to form a bigger, complete picture. When
you work a jigsaw puzzle, the pieces ultimately fit together only one way. Yet
there’s more than one way to arrive at the final picture. Your technique will
probably not be identical to that of a friend who puts the same puzzle together,
but the outcome is the same. Likewise in algebra, while there’s one final correct
answer, the way that you get that answer may not be identical to someone else’s.
But as long as you each follow the rules of algebra, your answers will be
equivalent.

Prerequisites

You should have completed one semester of Algebra I before taking this course.
If you did not take Math 11A through the Independent Study Program or you
used a different textbook in your first semester of Algebra at your school, you
may discover as you progress through the course that we covered some skills that
you didn’t get to in your course. If so, locate the appropriate topic from chapters
1–6 of the textbook and do some of the problems for those sections. Check your
answers in the back of the textbook.

Course Objectives and Content

Your first year of algebra is the foundation for geometry, higher-level algebra
courses, trigonometry, and calculus. By the completion of Math 12A, you’ll
be able to graph and use linear equations and inequalities; explore, graph, and
interpret nonlinear equations; perform operations with polynomials; graph and
solve systems of linear equations and inequalities; and demonstrate a basic
understanding of relations and functions. You’ll also see how these topics apply
to science, technology, sports, careers, consumer information, and other fields.

The course is comprised of written assignments, projects, and examinations.
There are seven written assignments, which you’ll turn in to be graded by your
instructor. You’ll also choose one project from a list to submit with each written
assignment after the first one. Three examinations, each emphasizing two to two
and a half chapters of the textbook, round out the course.

The following is a breakdown of each lesson’s content:

Lesson 1—Slopes and Equations of Lines
1A— Rate of Change
1B—The Slope of a Line
1C—Properties of Slope
1D—Slope-Intercept Equations for Lines
1E—Equations for Lines with a Given Point and Slope
1F— Equations for Lines Through Two Points

Lesson 2—Graphing Lines and Linear Inequalities; Exponents
2A—Fitting a Line to Data
2B—Equations for All Lines
2C—Graphing Linear Inequalities
2D—Compound Interest
2E—Exponential Growth
2F—Comparing Constant Increase and Exponential Growth
2G—Exponential Decay
2H—Chapter 7 Project

Lesson 3—Power Rules and Graphing Quadratic Equations
3A—Products and Powers of Powers
3B—Negative Exponents
3C—Quotients of Powers
3D—Powers of Products and Quotients
3E—Remembering Properties of Exponents and Powers
3F—Graphing y = ax^2
3G—Graphing y = ax^2 + bx + c
3H—Graphing Parabolas with an Automatic Grapher
3I—Quadratic Equations and Projectiles
3J—Chapter 8 Project

Lesson 4—First Exam (emphasizing lessons 1–3)

Lesson 5—Solving Quadratic Equations; Square Roots; Polynomials
5A—The Quadratic Formula
5B—Analyzing Solutions to Quadratic Equations
5C—Square Roots and Products
5D—Absolute Value, Distance, and Square Roots
5E—Distances in the Plane
5F—What Are Polynomials?
5G—Investments and Polynomials
5H—Multiplying a Polynomial by a Monomial
5I—Multiplying Polynomials
5J—Multiplying Binomials
5K—Special Binomial Products
5L—Chapters 9 and 10 Project

Lesson 6—Linear Systems
6A—An Introduction to Systems
6B—Solving Systems Using Substitution
6C—More Uses of Substitution
6D—Solving Systems by Addition
6E—Solving Systems by Multiplication
6F—Systems and Parallel Lines
6G—Situations Which Always or Never Happen
6H—Systems of Inequalities
6I—Chapter 11 Project

Lesson 7—Second Exam (emphasizing lessons 5–6)

Lesson 8—Factoring
8A—Factoring Integers into Primes
8B—Common Monomial Factoring
8C—Factoring x^2 + bx + c
8D—Solving Some Quadratic Equations by Factoring
8E—Factoring ax^2 + bx + c
8F—How Was the Quadratic Formula Found ?
8G—Rational Numbers and Irrational Numbers
8H—Which Quadratic Expressions Are Factorable?
8I—Chapter 12 Project

Lesson 9—Functions
9A—What Is a Function?
9B—Function Notation
9C—Absolute Value Functions
9D—Domain and Range
9E—Probability Functions
9F—Polynomial Functions
9G—The Tangent Function
9H—Functions on Calculators and Computers
9I—Chapter 13 Project

Lesson 10—Final Exam (emphasizing lessons 8 and 9)

Lesson 11—Cumulative Project Evaluation

Course Textbook

The course textbook is The University of Chicago School Mathematics Project:
Algebra, by John W. McConnell et al. This very readable textbook emphasizes the
application of algebra to everyday situations and shows the connection between
algebra and other topics in mathematics. We’ll study chapters 7–13 in this course.
(Chapters 1–6 were covered in Math 11A.)

The textbook is part of the University of Chicago School Mathematics Project
(UCSMP), which at this writing is celebrating its twentieth year of successful
teaching of pre-college math called. The project is supported by corporate and
foundation funding with the goal of having U.S. students gain mathematical
competence on a par with other countries, which have traditionally done better
in math than U.S. students. Students using this textbook and others in the series
score well on traditional standardized tests while doing better than other students
in problem solving and fields related to algebra such as statistics. The textbook’s
applications approach helps students make sense of algebraic ideas. The
Independent Study Program currently offers six courses covering pre-algebra,
algebra, and geometry based on these textbooks.

Other Course Materials

For this course you’ll need a notebook or loose-leaf binder of 8½-by-11-inch lined
paper, a ruler, graph paper, a scientific calculator, and an automatic grapher. An
automatic grapher called GCalc is included on a disk found in the pocket envelope
in the back of this learning guide. You’ll use this or another automatic grapher of
your choice.

Design of Lessons

Each nonexam lesson (except lesson 11) begins with a list of objectives, which
describe the skills you’ll learn in the lesson. Each nonexam lesson is then divided
into several study sessions, which contain the following parts:

• Reading Assignment—The reading assignment tells you which pages to
read in the course textbook. Go slowly and carefully through the reading
assignment before you read each study session’s discussion. Work out the
textbook examples in your notebook, making sure you understand the point
of each example.

• Discussion—The discussion clarifies the material in the reading assignment
and includes additional examples to help illustrate the topics covered in the
reading assignment. You’ll know that you’ve reached the end of an example
when you see this mark: .

• Practice Problems—These problems help you check your understanding of
the study session’s material. Do the practice problems before you do the study
session’s written assignment. Answers to these problems are located in the
answer section in the back of the textbook and in learning guide appendix A.
Do the practice problems on lined paper and keep them together in a notebook
or loose-leaf binder. Students who take the time to do the practice problems
tend to receive higher scores for the course than those who don’t.

• Written Assignment—Each study session ends with a written assignment
that you must complete and submit to your instructor for grading. Do the
written assignment problems on 8½-by-11-inch lined paper. Please write on
only one side of the paper and leave space between your answers. Be as neat
as possible since your instructor cannot grade material that can’t be read.
Include all work you do to answer each problem. Circle or box your final
answers to help your instructor locate them. If a problem requires graphing,
you must use graph paper and label the units and axes clearly on your graphs.
Some written assignments provide opportunities for extra credit.

The final study session in each nonexam lesson (except lessons 1 and 11) is a
chapter project in which you apply the concepts you learned in the lesson. From
a list of three projects, you must choose one project to complete and submit along
with the lesson’s written assignments. By the end of the course, you’ll have
completed six chapter projects. The five projects receiving the highest scores
will count toward your final course grade. Lesson 11, the cumulative project
evaluation, is where your final project grade will be recorded. We provide you
with the form that shows how your instructor will compute your final project
grade (as well as your overall course grade), but there is nothing for you to submit.
You will have already completed this lesson before you get to it. Your instructor
will include your overall project grade on the final examination cover sheet (with
your final examination grade and your overall course grade).

A written assignment checklist ends each nonexam lesson. Use this checklist to
double-check that you’ve done all of the lesson’s assigned problems before you
submit them for grading.

The Exams

Each of the course’s three exams emphasizes material from two or three textbook
chapters. Each exam consists largely of open-answer questions with some true/
false, multiple choice, or matching questions. All of the exams’ questions are
similar to the types of questions you’ll do in the written assignments. Lessons 4,
7, and 10 provide further details about the exams, as well as practice exams.

Grading Standards

The course’s written assignments are worth 40% of your final course grade (seven
written assignments worth 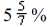each), your five best chapter projects are worth
15% of your course grade (3% each), and the three exams are worth 45% of your
course grade (15% each).

The grading scale for the course is as follows:

90 – 100% A
80 – 89%   B
70 – 79%   C
60 – 69%   D
 0 – 59%    F

Note: To be in compliance with the Independent Study Program’s academic
policies, your exam grades must average at least a D– in order for you to pass the
course. Even if your written assignment grades are excellent, you will not pass the
course unless you fulfill this requirement.

Plagiarism

As an educational institution, IU puts learning first. We want you to learn, and we
think you value learning as well. We also value honesty and trust. You have every
right to expect fair exams, fair assignments, and fair grades. By the same token,
your instructor expects the work you hand in to be your own. You are welcome to
discuss this course with other students and teachers, but when it comes to writing
your assignments, all the words should come straight from you, unless you are
supporting your assertions with a properly cited quote.

Passing off someone else’s work as your own is plagiarism. As stated in Indiana
University’s Code of Student Rights, Responsibilities, and Conduct (Art. III, §
A.3), “A student must not adopt or reproduce ideas, words, or statements of
another person without an appropriate acknowledgment. A student must give due
credit to the originality of others and acknowledge an indebtedness whenever he
or she does any of the following:

a. quotes another person’s actual words, either oral or written;
b. paraphrases another person’s words, either oral or written;
c. uses another person’s idea, opinion, or theory; or
d. borrows facts, statistics, or other illustrative material, unless the information
is common knowledge.”

We take plagiarism very seriously. If you are caught plagiarizing, you could
receive an F for the whole course.

So how can you avoid plagiarizing? When is it appropriate to cite your sources,
and how should you cite them? The answer’ s simple . Ask your instructor. If
you’re unsure whether you’ve cited your sources appropriately, call or e-mail
your instructor before you submit your assignment. Not only will you get answers
to your questions, you’ll reap the fruit of honesty: trust.

Contacting Your Instructor

With each lesson you are required to submit an assignment cover sheet. Every
assignment cover sheet has a space for your questions and comments; you are
strongly encouraged to use this space. If problems arise between assignments, you
can write to your instructor at the Independent Study Program. Many instructors
can be contacted via e-mail or reached by telephone during established office
hours. To learn your instructor’s e-mail address and/or office hours, please refer
to the contact information on the back cover of this learning guide.

Some Tips before We Begin

Studying mathematics is different from studying other subject areas. All those
jumbles of numbers can look confusing. Don’t give up• It’s important that you pay
attention to those jumbles in the examples in the textbook and learning guide. Try
to figure out what’s different from one step in the example to the next, and then
ask yourself how or why what was done was done. Look at other examples for
similar steps.

If you begin to get frustrated, don’t throw the textbook or break your pencil. (My
favorite stress reliever in high school was to bite my pencil. Sometimes I didn’t
realize how stressed I was until I noticed that I had nearly bitten my pencil in half•
Then I knew I needed to take a break.) Get away from the problem for a few hours
or even a day. When you come back, things will probably be clearer. If you’re still
confused after you return to the problem, ask someone for help. You may also
contact your instructor, who’ll be happy to explain the material to you. Just be
sure when you contact your instructor to have the problem in front of you,
including the scratch work you did to try to figure out the problem. This process
of trying to understand the material, as well as the jumbles of numbers and steps,
are part of putting together the puzzle of algebra.

While there are a lot of numbers on the pages, the words are important too.
Learning algebra is like learning any language. You must learn the vocabulary of
algebra to succeed in algebra. If you can’t understand what you’re being asked to
do, how can you do it? Reread material that doesn’t make sense the first time.
Look at the textbook and learning guide examples to see how the words explain
what’s being done with the numbers. Again, if you still can’t figure it out, ask
someone for help.

Choose to work in an environment that enhances learning for you. I prefer to study
mathematics with music in the background, but you might require absolute silence
when studying math. (I require a quiet environment when I’m writing papers or
trying to comprehend most science courses.) You may like working in a cool
room to help you think, or you might prefer (as I do) a slightly warmer room (but
not too warm; you might fall asleep). Maybe you like a very bright room. Perhaps
you need an orderly, organized, almost sterile desk with no materials other than
your math book and papers on it. If you’re a morning person, try working on your
math as early as you can each day; if you’re a night owl, work in the evenings.
The point is that you need to find out what helps promote learning for you and try
to achieve that environment to the best of your ability each time you study. If you
don’t already know what you prefer, try some of the environments and times
mentioned above until you find the combination that seems to work best for you.

And now, let’s work on putting together the puzzle of algebra•