mathematics standards to grade 5
Standard 1 — Number Sense
Understanding the number system is the basis of mathematics. Students extend
their understanding of the magnitudes of numbers to rounding whole numbers and
decimals to any place value. They order and compare whole numbers and decimals
using the correct symbols for greater than and less than. They develop the
concept of percentage as parts of a hundred and compare different ways of
looking at fractions. They identify whole numbers as prime or composite, and
they compare fractions, decimals, and mixed numbers on a number line.
Standard 2 — Computation
Fluency in computation is essential. Students extend the standard methods for
multiplying and dividing to larger numbers. They add and subtract more complex
fractions and decimals, learning how these different representations of numbers
can be manipulated. They also develop an understanding of how to multiply and
divide fractions.
Standard 3 — Algebra and Functions
Algebra is a language of patterns, rules, and symbols. Students at this level
develop further the fundamental concept of a variable — having a letter stand
for all numbers of a certain kind. They use this to write simple algebraic
expressions and to evaluate them. They begin to develop the idea of linking an
algebraic equation to a graph, by finding ordered pairs that fit a linear
equation, plotting these as points on a grid, and drawing the resulting straight
line. They also interpret graphs to answer questions.
Standard 4 — Geometry
Students learn about geometric shapes and develop a sense of space. They draw
angles, parallel and perpendicular lines, the radius and diameter of circles,
and other geometric shapes, using ruler, compass, protractor, and computer
drawing programs. They identify congruent triangles and explain their reasoning
using specific geometrical terms , such as equilateral, isosceles, acute, and
obtuse. They classify polygons with five or more sides. They develop an
understanding of reflectional and rotational symmetry, and they construct prisms
and pyramids, developing their ability to work in three dimensions.
Standard 5 — Measurement
The study of measurement is essential because of its uses in many aspects of
everyday life. Students develop and use the formulas for calculating perimeters
and areas of triangles, parallelograms, and trapezoids. They extend these ideas
to finding the volume and surface area of rectangular solids. They understand
and use additional units for measuring weight: ounce, gram, and ton. They also
add and subtract with money in decimal notation.
Standard 6 — Data Analysis and Probability
Data are all around us — in newspapers and magazines, in television news and
commercials, in quality control for manufacturing — and students need to learn
how to understand data. At this level, they use the mean, median, mode, and
range to describe data sets. They further develop the concept of probability,
recording probabilities as fractions between 0 and 1 and linking these to levels
of certainty about the events described.
Standard 7 — Problem Solving
In a general sense, mathematics is problem solving. In all of their mathematics,
students use problem-solving skills: they choose how to approach a problem, they
explain their reasoning, and they check their results. As they develop their
skills with algebra, geometry, or measurement, for example, students move from
simple to more complex ideas by taking logical steps that build a better
understanding of mathematics.
As part of their instruction and assessment, students should also develop the
following learning skills by Grade 12 that are woven throughout the mathematics
standards:
Communication
The ability to read, write, listen, ask questions, think, and communicate about
math will develop and deepen students’understanding of mathematical concepts.
Students should read text, data, tables, and graphs with comprehension and
understanding. Their writing should be detailed and coherent, and they should
use correct mathematical vocabulary. Students should write to explain answers,
justify mathematical reasoning, and describe problem-solving strategies.
Reasoning and Proof
Mathematics is developed by using known ideas and concepts to develop others.
Repeated addition becomes multiplication. Multiplication of numbers less than
ten can be extended to numbers less than one hundred and then to the entire
number system. Knowing how to find the area of a right triangle extends to all
right triangles. Extending patterns, finding even numbers, developing formulas,
and proving the Pythagorean Theorem are all examples of mathematical reasoning.
Students should learn to observe, generalize, make assumptions from known
information, and test their assumptions.
Representation
The language of mathematics is expressed in words, symbols, formulas, equations,
graphs, and data displays. The concept of one-fourth may be described as a
quarter, 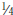 , one divided by four, 0.25,
, one divided by four, 0.25,
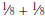 , 25 percent, or an
appropriately shaded portion of a pie graph. Higher-level mathematics involves
the use of more powerful representations: exponents , logarithms,
, 25 percent, or an
appropriately shaded portion of a pie graph. Higher-level mathematics involves
the use of more powerful representations: exponents , logarithms,
 , unknowns,
statistical representation, algebraic and geometric expressions. Mathematical
operations are expressed as representations: +, =, divide, square.
Representations are dynamic tools for solving problems and communicating and
expressing mathematical ideas and concepts.
, unknowns,
statistical representation, algebraic and geometric expressions. Mathematical
operations are expressed as representations: +, =, divide, square.
Representations are dynamic tools for solving problems and communicating and
expressing mathematical ideas and concepts.
Connections
Connecting mathematical concepts includes linking new ideas to related ideas
learned previously , helping students to see mathematics as a unified body of
knowledge whose concepts build upon each other. Major emphasis should be given
to ideas and concepts across mathematical content areas that help students see
that mathematics is a web of closely connected ideas (algebra, geometry, the
entire number system). Mathematics is also the common language of many other
disciplines (science, technology, finance, social science, geography) and
students should learn mathematical concepts used in those disciplines. Finally,
students should connect their mathematical learning to appropriate real-world
contexts.
Standard 1
Number Sense
Students compute with whole numbers*, decimals, and fractions and understand the
relationship among decimals, fractions, and percents. They understand the
relative magnitudes of numbers. They understand prime* and composite* numbers.
5.1.1
Convert between numbers in words and numbers in figures, for numbers up to
millions and decimals
to thousandths.
Example: Write the number 198.536 in words.
5.1.2
Round whole numbers and decimals to any place value.
Example: Is 7,683,559 closer to 7,600,000 or 7,700,000? Explain your answer.
5.1.3
Arrange in numerical order and compare whole numbers or decimals to two
decimal places by using
the symbols for less than (<), equals (=), and greater than (>).
Example: Write from smallest to largest: 0.5, 0.26, 0.08.
5.1.4
Interpret percents as a part of a hundred. Find decimal and percent
equivalents for common fractions
and explain why they represent the same value.
Example: Shade a 100-square grid to show 30%. What fraction is this?
5.1.5
Explain different interpretations of fractions: as parts of a whole, parts
of a set, and division of whole
numbers by whole numbers.
Example: What fraction of a pizza will each person get when 3 pizzas are divided
equally
among 5 people?
5.1.6
Describe and identify prime and composite numbers.
Example: Which of the following numbers are prime: 3, 7, 12, 17, 18? Justify
your choices.
5.1.7
Identify on a number line the relative position of simple positive
fractions, positive mixed numbers,
and positive decimals.
Example: Find the positions on a number line of 1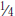 and 1.4.
and 1.4.
* whole number: 0, 1, 2, 3, etc.
* prime number: a number that can be evenly divided only by 1 and itself (e.g.,
2, 3, 5, 7, 11)
* composite number: a number that is not a prime number (e.g., 4, 6, 8, 9, 10)
Standard 2
Computation
Students solve problems involving multiplication and division of whole numbers
and solve problems involving addition, subtraction, and simple multiplication
and division of fractions and decimals.
5.2.1
Solve problems involving multiplication and division of any whole numbers.
Example: 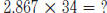 . Explain your method.
. Explain your method.
5.2.2
Add and subtract fractions (including mixed numbers) with different
denominators .
Example: 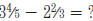 .
.
5.2.3
Use models to show an understanding of multiplication and division of
fractions.
Example: Draw a rectangle 5 squares wide and 3 squares high. Shade
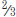 of the
rectangle, starting
from the left. Shade
of the
rectangle, starting
from the left. Shade 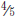 of the rectangle, starting from the top. Look at the
fraction of the squares
that you have double -shaded and use that to show how to multiply
of the rectangle, starting from the top. Look at the
fraction of the squares
that you have double -shaded and use that to show how to multiply
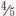 by
by 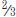 .
.
5.2.4
Multiply and divide fractions to solve problems.
Example: You have 3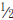 pizzas left over from a party. How many people can have
pizzas left over from a party. How many people can have
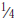 of a pizza each?
of a pizza each?
5.2.5
Add and subtract decimals and verify the reasonableness of the results.
Example: Compute 39.46 -20.89 and check the answer by estimating.
5.2.6
Use estimation to decide whether answers are reasonable in addition,
subtraction, multiplication,
and division problems.
Example: Your friend says that 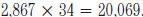 . Without solving, explain why
you think
the answer is wrong.
. Without solving, explain why
you think
the answer is wrong.
5.2.7
Use mental arithmetic to add or subtract simple decimals.
Example: Add 0.006 to 0.027 without using pencil and paper.
Standard 3
Algebra and Functions
Students use variables in simple expressions, compute the value of an expression
for specific values of the variable, and plot and interpret the results. They
use two-dimensional coordinate grids to represent points and graph lines.
5.3.1
Use a variable to represent an unknown number.
Example: When a certain number is multiplied by 3 and then 5 is added, the
result is 29.
Let x stand for the unknown number and write an equation for the relationship.
5.3.2
Write simple algebraic expressions in one or two variables and evaluate
them by substitution.
Example: Find the value of 5x +2 when x t =3.
5.3.3
Use the distributive property* in numerical equations and expressions.
Example: Explain how you know that 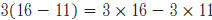 .
.
5.3.4
Identify and graph ordered pairs of positive numbers.
Example: Plot the points (3, 1), (6, 2), and (9, 3). What do you notice?
5.3.5
Find ordered pairs (positive numbers only) that fit a linear equation ,
graph the ordered pairs,
and draw the line they determine.
Example: For x = 1, 2, 3, and 4, find points that fit the equation y =2x
+ 1.
Plot those points
on graph paper and join them with a straight line.
5.3.6
Understand that the length of a horizontal line segment on a coordinate
plane equals the difference
between the x-coordinates and that the length of a vertical line segment on a
coordinate plane equals
the difference between the y-coordinates.
Example: Find the distance between the points (2, 5) and (7, 5) and the distance
between
the points (2, 1) and (2, 5).
5.3.7
Use information taken from a graph or equation to answer questions about a
problem situation.
Example: The speed (v feet per second) of a car t seconds after it starts is
given by the formula
v = 12t. Find the car’s speed after 5 seconds.
* distributive property: e.g.,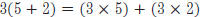
| Prev | Next |