Operations on Imaginary Numbers

PLEASE NOTE THAT YOU CANNOT USE A CALCULATOR ON THE ACCUPLACER -
ELEMENTARY ALGEBRA TEST! YOU MUST BE ABLE TO DO THE FOLLOWING PROBLEMS
WITHOUT A CALCULATOR!

Simplifying Square- Root Radicals Containing Perfect Square Factors

Some radicands are perfect squares , whereas others are not. In the later case it is often
useful to "simplify" the radicand IF it contains a perfect-square factor!

•If the radicand is a perfect square, find its square root.
•If the radicand is not a perfect square, try to factor the radicand so that one factor is
the largest possible perfect square factor. Place the square root of this factor
outside the radical and keep the other factors inside (or under) the radical. There is
an assumed multiplication sign between the number outside the radical and
and the radical expression.
•If the radicand is not a perfect square and it does not have a perfect square factor,
then it is simplified.

Problem 1:

Simplify .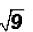

The word "simplify" takes on many meanings in mathematics. Often you must
figure out its meaning from the mathematical expression you are asked to
"simplify." Here we are asked to "simplify" instead of finding the square root.

Since the radicand is a perfect square, we can say 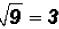. This is NOT an irrational
number.

Problem 2:

Simplify .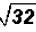

The word "simplify" takes on many meanings in mathematics. Often you must
figure out its meaning from the mathematical expression you are asked to
"simplify." Here we are asked to "simplify" instead of factoring out perfect-square
factors.

Here the radicand is not a perfect square. However, we know that we can write the
radicand as a product as follows :



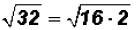
Since we know that 16 is a perfect square and it is also the largest perfect square factor
of the radicand, we can now simplify the square root.

That is,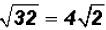 in simplified form.

Please note that 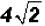means 4 times the .

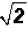Problem 3:

Simplify .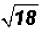

Here the radicand is not a perfect square. However, we know that we can write the
radicand as a product as follows:



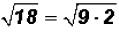
Since we know that 9 is a perfect square and it is also the largest perfect square factor of
the radicand, we can now simplify the square root.

That is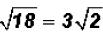, in simplified form.


Problem 4:

Simplify.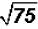

Here the radicand is not a perfect square. However, we know that we can write the
radicand as a product as follows:

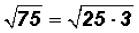
Since we know that 4 is a perfect square and it is also the largest perfect square factor of
the radicand, we can now simplify the square root.

That is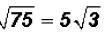, in simplified form.
 

Problem 5:

Simplify .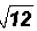

Here the radicand is not a perfect square. However, we know that we can write the
radicand as a product as follows:

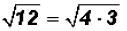
Since we know that 4 is a perfect square and it is also the largest perfect square factor of
the radicand, we can now simplify the square root.

That is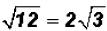, in simplified form.

Problem 6:

Simplify .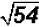

Here the radicand is not a perfect square. However, we know that we can write the
radicand as a product as follows:



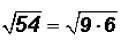
Since we know that 9 is a perfect square and it is also the largest perfect square factor of
the radicand, we can now simplify the square root.

That is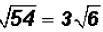, in simplified form.

Adding and Subtracting Square -Root Radicals

Add or subtract the coefficients of like radicals .
Use the common radical as a factor in the solution.

Problem 7:

Add 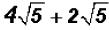and simplify, if possible.

The word "simplify" takes on many meanings in mathematics. Often you must
figure out its meaning from the mathematical expression you are asked to
"simplify." Here we are asked to "simplify" instead of factoring perfect-square
factors out of the sum.

Since both terms have the same radical we can add their coefficient to get

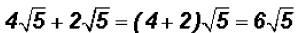
Problem 8:

Add 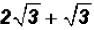and simplify, if possible.

Please note that there is an implied coefficient of 1 in front of 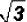. It is NOT customary to
write it. However, it must be used in addition and subtraction!

Since both terms have the same radical we can add their coefficient to get

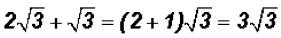
Problem 9:

Combine the "like" radicals in 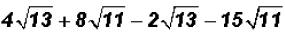and simplify, if
possible.

The word "simplify" takes on many meanings in mathematics. Often you must
figure out its meaning from the mathematical expression you are asked to
"simplify." Here we are asked to "simplify" instead of factoring perfect-square
factors out of the result

Let's rearrange the expression as follows and then combine the terms with like radicals.
That is,

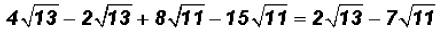
Pleasenote that we cannot add the coefficients of the final difference! There are no like
radicals and the radicands are prime numbers.

Problem 10:

Subtract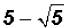 and simplify, if possible.

The word "simplify" takes on many meanings in mathematics. Often you must
figure out its meaning from the mathematical expression you are asked to
"simplify." Here we are asked to "simplify" instead of factoring perfect-square
factors out of the difference.

No simplification can take place. The only thing that could be done is to change the
radical to a rounded decimal number and then subtract.

Problem 11:

Subtract 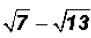and simplify, if possible.

No simplification can take place. The only thing that could be done is to change the
radicals to rounded decimal numbers and then subtract.

Problem 12:

Add 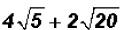and simplify, if possible.

There are no like radicals. However, 20 is NOT a prime number, therefore, we can
simplify the second radical to see if we end up with a sum of like radicals .

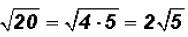and we find that we DO have like radicals when simplifying!

Now we can write

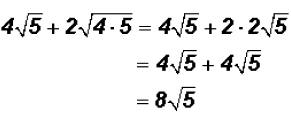
Problem 13:

Subtract 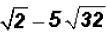and simplify, if possible.

There are no like radicals. However, 32 is NOT a prime number, therefore, we can
simplify the second radical to see if we end up with a difference of like radicals.

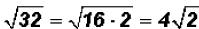and we find that we do have like radicals when simplifying!

Now we can write

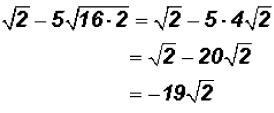
Please note that there is an implied coefficient of 1 in front of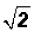 . It is NOT customary to
write it. However, it must be used in addition and subtraction!

Problem 14:

Subtract 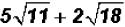and simplify, if possible.

There are no like radicals. However, 18 is NOT a prime number, therefore, we can
simplify the second radical to see if we end up with a sum of like radicals.

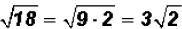and we find that we still DO NOT have like radicals when
simplifying!

However, we might want to write

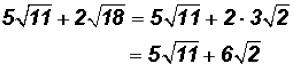
Please note that we cannot add the coefficients of the final difference! There are no like
radicals and the radicands are now prime numbers.

Multiplying Square-Root Radicals

•Multiply the coefficients.
•Multiply the radicands.
•Simplify, if possible.

Symbolically , this can be stated as .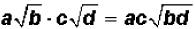

Problem 15:

Multiply 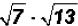and simplify, if possible.

The word "simplify" takes on many meanings in mathematics. Often you must
figure out its meaning from the mathematical expression you are asked to
"simplify." Here we are asked to "simplify" instead of factoring perfect-square
factors out of the product.

The coefficients are both 1. But we can multiply the radicands as follows:
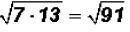. The radical cannot be simplified because 91 is a prime number.

Problem 16:

Multiply 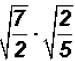and simplify, if possible.

The coefficients are both 1. But we can multiply the radicands as follows:
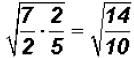. The product can be reduced!
That is,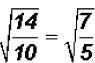 which cannot be simplified.

Problem 17:

Multiply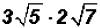 and simplify, if possible.
The coefficients are 3 and 2. Therefore, they need to be multiplied as well as the
radicands.

That is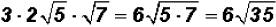 . The radical cannot be simplified because 35
is a prime number.

Problem 18:

Multiply 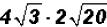and simplify, if possible.
The coefficients are 4 and 2. Therefore, they need to be multiplied as well as the
radicands.

That is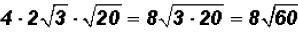 . The radical is NOT a prime number and
we may be able to simplify it.

That is,

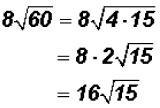
Problem 19:

Multiply 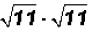and simplify, if possible.

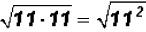and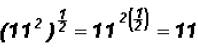

NOTE: Whenever you multiply a radical by itself, the solution is ALWAYS the
radicand!

Problem 20:

Multiply 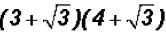and simplify, if possible.

Here we have to use the FOIL process. Remember that FOIL stands for First Product,
Outer Product, Inner Product, and Last Product.

That is,

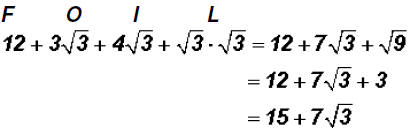
Please note that the two middle products have like radicands that is why we added their
coefficients!

Problem 21:

Multiply 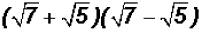and simplify, if possible.
Here we have to use the FOIL process again.

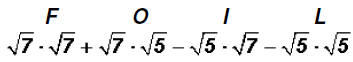
Please note the following: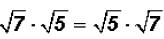

Since the two middle products have the same value, they cancel each other out when one
is subtracted from the other!

Therefore, we get

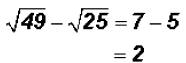
Dividing Square -Root Radicals

Divide the coefficients.
Divide the radicands.
Simplify, if possible.
Symbolically, this can be stated as .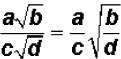

Problem 22:

Divide 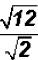and simplify, if possible.

The word "simplify" takes on many meanings in mathematics. Often you must
figure out its meaning from the mathematical expression you are asked to
"simplify." Here we are asked to "simplify" instead of factoring perfect-square
factors out of the quotient.

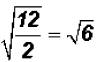The radical cannot be simplified because 6 does not contain a perfectsquare
factor.

Problem 23:

Divide 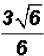and simplify, if possible.

The coefficient 3 in the numerator and the denominator 6 can be divided (or reduced)
because they are both outside the radical. NOTE: You cannot divide the 6 under the
radical by the 6 in the denominator !

We get 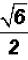. The coefficient 1 in the numerator is implied! The radical cannot be
simplified because 6 does not contain a perfect-square factor.

Problem 24:

Divide 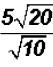and simplify, if possible.
We get 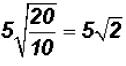. The radical cannot be simplified because 2 is a prime number.

Rationalizing a Denominator containing an Irrational Square-Root Radical

•Multiply the denominator by itself.
•To preserve the value of the fraction, multiply the numerator by the same number.
•Simplify all radicals and reduce the resulting fraction, if possible.

NOTE: In Steps 1 and 2 above , we have actually multiplied the fraction by an
equivalent of the number 1!

Problem 25:

Rationalize the denominator in 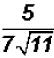and simplify, if possible.

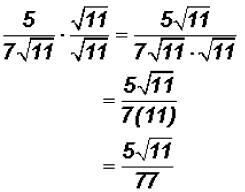
The radical cannot be simplified because 11 is a prime number.

Remember 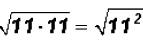that and 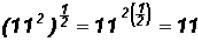. Also .

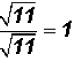NOTE: You cannot divide the 77 in the denominator by the 11 in the radical!

Problem 26:

Rationalize the denominator in 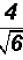and simplify, if possible.

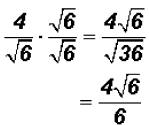. The radical cannot be simplified because 6 does not contain a
perfect-square factor.

NOTE: You cannot divide the 6 under the radical by the 6 in the denominator !

However, the coefficient 4 in the numerator and the denominator 6 can be reduced
because they are both outside the radical.

That is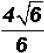, can be written as 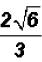. You cannot divide the 6 under the radical by
the 3 in the denominator !

Problem 27:

Rationalize the denominator in 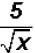and simplify, if possible.

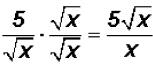
NOTE: You cannot divide the x under the radical by the x in the denominator !

Problem 28:

Rationalize the denominator in 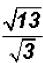and simplify, if possible.

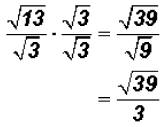
The radical cannot be simplified because 39 does not contain a perfect-square factor.
NOTE: You cannot divide the 39 under the radical by the 3 in the denominator !

Problem 29:

Rationalize the denominator in 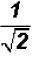and simplify, if possible.

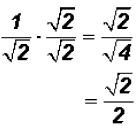
The radical cannot be simplified because 2 is a prime number.

NOTE: You cannot divide the 2 under the radical by the 2 in the denominator !

Problem 30:

Rationalize the denominator in 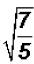and simplify, if possible.

First we need to be aware of the following:

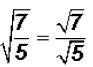
Now we can rationalize the denominator as usual.

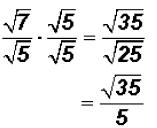
The radical cannot be simplified because 35 does not contain a perfect-square factor.

NOTE: You cannot divide the 35 under the radical by the 5 in the denominator !