Problem Set 1: Math Basics

Objective: In this section you will do simple calculations using numbers in power-of-ten also referred to as exponential notations or
scientific notation. You will then learn how to 1) apply the rules for rounding off and 2) apply the rules of significant figures when
performing mathematical calculations.

Discussion
I. Writing numbers in Powers -of-ten.
1. The power -of-ten form of writing a number is a shorthand method of writing a very large or a very small number.

Example: Positive Exponent

a. 1000 = 1 x 10 x 10 x 10 or 1000 = 1 x 10³
b. 10,000 = 1 x 10 x 10 x 10 x 10 or 10,000 = 1 • 10⁴

In the number 10⁴, 10 is called the base and 4 is called the exponent.

Negative Exponent
c. 0.001 = 1 x 1/10 x 1/10 x 1/10 or 0.001 = 1 • 10^-3 (negative exponent)
d. 0.000001 = 1 x 1/10 x 1/10 x 1/10 x 1/10 x 1/10 x 1/10 or 0.000001 = 1 • 10^-6
The zero before the digit is dropped , and the number in power-of-ten form becomes 1 • 10^-6.
10 is called the base and -6 is called the exponent.

2. The method of writing a number in power-of-ten form is simply to move decimal point so that there is only one digit to the left
of the decimal point. Counting the number of spaces the decimal point is moved from its original location determines the
exponent.

Example There is an implied decimal point at the end of a whole number. For example, 100 can be written 100. To
put this number in power-of-ten form, move the decimal point so that only one digit remains to the left of
it. 100. → 1.00 Since the decimal point is moved two places to the left, the exponent becomes 2 on
the base 10, or 1.00 x 10². Final zeros may be dropped if the number is not a measurement. (Later in
this exercise you will learn rules for dropping zeros.) The number 1.00 x 10² is usually written as 1 • 10².

For negative exponents, the decimal is moved to the right. 0.0010→ 0001.0. Since the decimal point three
places to the right so the exponent becomes -3 on the base 10, or 1.0 x 10^-3.

3. So far we have looked only at numbers that begin with the digit 1. Numbers beginning with any digit or set of digits can be
placed in power-of-ten form.

Example a. (200) is (200.). The decimal point is moved so that only one digit remains to the left of the decimal place:
(200.) becomes (2.00). The number of places the decimal is moved becomes the exponent. The number is
written: 2.00 x 10² → 2 x 10²

b. (9050) is (9050.) with decimal point at the end. 9050. → 9.050 when moving the decimal point three
places to the right. The number is 9.05 • 10³.

4. Decimal numbers can also be expressed in power-of-ten form. The same rules apply as in whole numbers: Move the decimal
point so that only one digit remains to the left of the decimal point. Counting the number of spaces the decimal point is moved
determines the exponent for the number expressed in power-of-ten. If the decimal point is moved to the right, (i.e., the number
is less than one) then there is a negative sign associated with the exponent when expressed in power-of-ten form.

Example a: (0.012) is (01.2). The decimal point was moved two places to the right so the exponent becomes -2. (The
minus sign on the exponent tell us that this is the power-of-ten form of a decimal number.) The zero before
the digit is dropped, and the number in power-of-ten form becomes 1.2 x 10^-2.

b: (0.00062) becomes (0006.2). The exponent is -4 and the number is 6.2 • 10^-4. The zeros before the 6
are dropped.

Math operations using power -of-ten

1. Multiplying numbers in power-of-ten form involves two steps.
Step 1: First multiply the two initial digits.

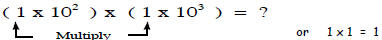
Step 2: Multiply the numbers with exponents by adding the exponents . Put the signs in front of the exponents
when adding.

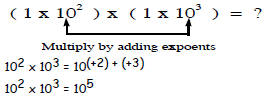
Now combine the answers from both steps

(1•10²) x (1•10³) = 1•10⁵

2. Dividing numbers in power-of-ten form also occurs in two steps.
Step 1: Divide the initial digit in the numerator by the initial
digit in the denominator.

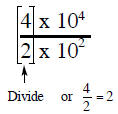
Step 2: Divide the numbers with exponents by subtracting the exponents in the denominator from the exponent in
the numerat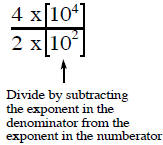or.

or

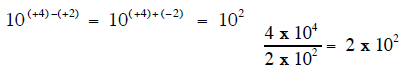
Now combine the answers from
both side

II Rounding off numbers.

1. When a number is rounded off to a given place, the digit immediately to the right of that place tells us what to do. If the
digit to the immediate right is 5, 6, 7, 8, or 9, then 1 is added to the digit that is being rounding to and all digits to the right is
dropped. If the digit to the immediate right is 1,2,3 or 4, then the digit stays intact and all digits to the right is dropped.

Example: a. The number 2.489 is to be rounded off to the tenths place

2.489
(rounded off to the tenths place) = 2.5

Example b. The number 0.0925 is rounded off to the hundredths place. 0.0925 = 0.09

Example c. The number 0.00449 is rounded off to the thousandths place. 0.00449 = 0.004

Consider a number such as 123.45678. Here the digit 4 is in the tenth place, the digit 5 is in the hundredth place, the digit six is in the
thousandth place, and so on. In short for any number with the following format: V W X Y Z in which V, W, X, Y and Z are digit and
the decimal is between the V and W digit, then the tenth digit is represented by W, the hundredth represented by X, the thousand
represented by Y, ten-thousandth represented by Z and so on.

III Determining significant figures

1. There are rules for determining what digits are significant in a number. All nonzero digits are significant.
Example a.

 i. 897 has three significant figures.
ii. 58.62 has four significant figures.

2. Not all digits in a number are significant; some digits are only placeholders.
Example b.

 In the number 0.0097, all digits to the left of the 9 are placeholders and therefore not
significant. 0.0097 has two significant figures

3. Zeros at the left of a measurement are not significant.
Example c.

i. 0.0017 has only two significant figures; the 1 and 7.
ii. 0.193 has three significant figures.

4. Zeros between nonzero digits are significant.
Example d.

i. 903 has three significant figures.
ii. 1.0004 has five significant figures.
iii. 0.02004 has four significant figures.

5. Zeros at the right end of a number, after a decimal point, are significant.
Example e.

i. 0.400 has three significant figures.
ii. 0.0090 has two significant figures.
iii. 5.000 has four significant figures.

6. Zeros to the right of a nonzero digit but before the decimal point may or may not be significant.
Example f.

i. 400 (The zeros may not be significant)
ii. 6000 (The zeros may not be significant )
In this course you may assume that these digits are not significant, unless told so by your
instructor.

Math operations using significant figures

1. In addition and subtraction, the final answer must not be more precise (i.e., numbers with more digits to the right of the
decimal) than the data with the least precision .

Example a. 4.732 - 3.62 = 1.112 but the answer must be expressed to only the hundredths decimal place
because the hundredths decimal place is the smallest place on the number 3.62 (which is the
least precise of the data being added); hence, the answer is 1.11.

Example b. 17.8 + 14.73 + 16 = 48.53 rounded to 49. (the number 16 is the least precise of the data)

2. In multiplying and dividing measurements, an answer cannot have more significant digits than the measurement with the
least number of significant digits used to arrive the answer.

Example a.

The answer has been rounded off to three significant figures because 1.64 has only three
significant figures. The answer must also contain three significant figures.

Example b. 58.7 ÷ 2.4 = 24.458 but the answer must be rounded off to two significant figure, or 24.

I. For part 1 & 2 below, write all answers in terms of the Powers -of-ten with the correct number of significant figures.

Write the following number in power-of-10 form.
i.e1., 65,000 = 6.5 e⁺⁴ or 6.5 e⁴
i.e2., 0.00065 = 6.5 e^-4

When typing in your answer use a format in which your answer has a space (blank) between the number (6.5) and the "e"
(representing the exponent) thus in the first example 65,000 is written as 6.5 e⁺⁴ or 6.5 e⁴. In the second example, 0.00065
is written as 6.5 e^-4

a (1). 1000 ___________ b (2). 1,000,000 ___________
c (3). 1 ___________ d (4). 909,000 ___________
e (5). 67,000,000 ___________ f (6). 0.001 ___________
g (7). 0.01 ___________ h (8). 0.00028 ___________
i (9). 0.00306 ___________ j (10). 0.000000614 ___________

II Math operations using power-of-ten: Calculate each and then write your answers in powers-of-ten.
Write the following number in power-of-10 form.
i.e1., 65,000 = 6.5 e⁺⁴ or 6.5 e⁴
i.e2., 0.00065 = 6.5 e^-4

When typing in your answer use a format in which your answer has a space (blank) between the number (6.5) and the "e"
(representing the exponent) thus in the first example 65,000 is written as 6.5 e⁺⁴ or 6.5 e⁴. In the second example, 0.00065
is written as 6.5 e^-4

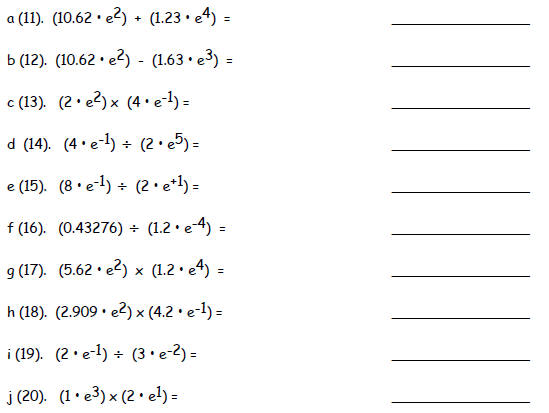
III. Rounding off each number below according to the directions.
Recall for a number with the format V . W X Y Z , the digits W is in the tenth place, the digit X is in
the hundredth place, the digit Y is in the thousandth place and so on.

a (21). Round to the tenth place: 21.246 = ___________
b (22). Round to the hundredths place: 482.0146 = __________
c (23). Round to the thousandths place: 4.126879 = _________
d (24). Round to the ten-thousandths place: 1.00035 = __________
e (25). Round to the hundredths place: 21.2554 = __________

IV. Significant figures.
Write the number of significant figures for each of the number below. i.e., 34.02 has 4 sig. figs.
a (26). 0.0082 ___________ b (27). 907 ___________
c (28). 201 ___________ d (29). 45000 ___________
e (30). 0.010 ___________ f (31). 6.090 ___________
g (32). 914 ___________ h (33). 6.00 ___________
i (34). 400020 ___________ j (35). 0.000000614 ___________

V. Math operations using significant figures.
Write the following number in power-of-10 form.
i.e1., 65,000 = 6.5 e⁺⁴or 6.5 e⁴
i.e2., 0.00065 = 6.5 e^-4

When typing in your answer use a format in which your answer has a space (blank) between the number (6.5) and the "e"
(representing the exponent) thus in the first example 65,000 is written as 6.5 e⁺⁴4 or 6.5 e⁴4. In the second example, 0.00065
is written as 6.5 e^-4

Answer the following using the correct number of significant figures. Write the complete answers
first then the rounded-off number and write this answer in the parenthesis .

a (36). 2.0 + 3.88 5.88 . (_5.9_) b (37). 34.000 - 2.15 _________ (_______)
c (38). 6.944 - 3.3 ___________ (_______) d (39). 100 + 204.45 _________ (_______)
e (40). 5.386 x 2.11 ___________ (_______) f (41). 68.00 ÷ 24.0 _________ (_______)
g (42). 0.6140 ÷ .093 ___________ (_______) h (43). 2.3•e^-3 x 2.501 _________ (_______)
i (44). 1.32•e⁶ ÷ 0.61 ___________ (_______) j (45). 4500 x 2.6789•e² _________ (_______)