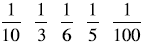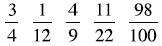Rational Number Project
Understandings
But with enough experiences with concrete models, students
do overcome these
misunderstandings. Below find student examples for the transitive and residual
strategies:
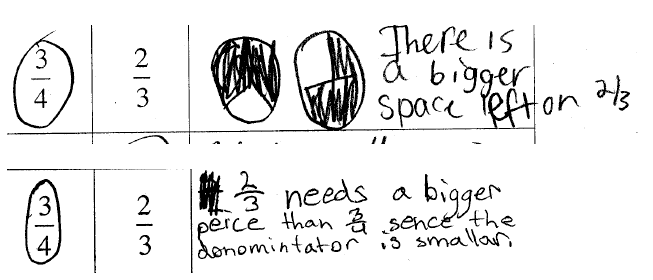
When you teach lesson 3 you will notice students using these informal ordering
strategies along
with other benchmarks to estimate fraction and subtraction problems effectively.
Order these fractions from smallest to
largest. Be prepared to explain your
thinking.
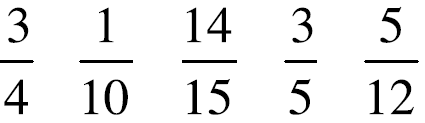
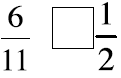
Picture these fractions in your mind . Is the fraction
greater than ½ or less than ½? Put a > or < sign
in each box to show your answer. When in doubt use fraction circles or draw
pictures to help you
decide if the fraction is more or less than 1-half.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
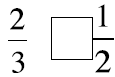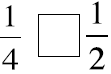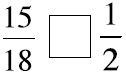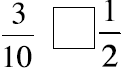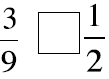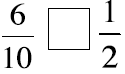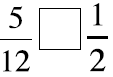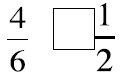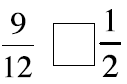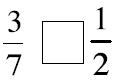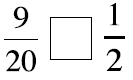Complete these fractions so they are all close to 2/3 , but just a bit bigger.
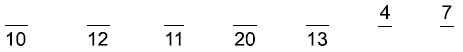
Fraction Estimation
Work with a partner to order the fractions in each set
from smallest to largest. Explain your
thinking to each other.
 |
 |
 |
 |
 |
 |
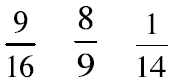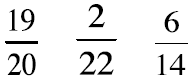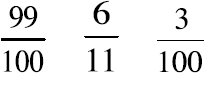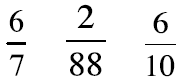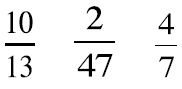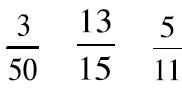Which fraction is the smallest?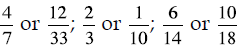 
Which fraction is the largest?
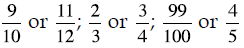
On the back of this paper, describe your strategies for
ordering these last two
fraction pairs.
Estimate the amount shaded in each example:
Shade to show about 4/7
Shade to show about 18/40
| Order from smallest to largest. Explain your reasoning:
|
Picture each fraction. What fraction away from one whole is each one? 10/11 is ___ away from one whole. Which fraction is larger? 10/11 or 6/7 |
| Margo and Joshua both had a candy bar (same size). Margo ate about 2/3 of her candy bar. Joshua ate about 5/12 of his candy bar. Who ate less? How do you know? |
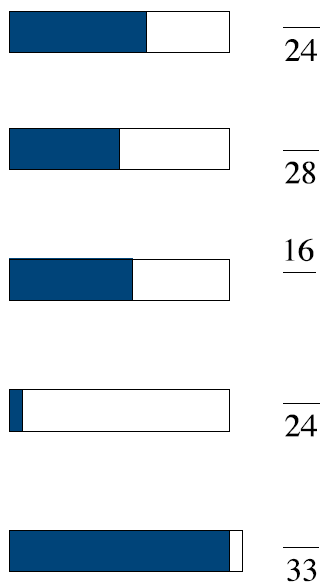
Ruby ran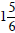 
miles. Robert ran 1 miles.How much further would Ruby need to run to run 2 miles? How much further would
Robert need to Who ran the furthest? Ruby or Robert? |
| If you live 2/8 of a mile from school And you friend lives 2/5 of a mile, who lives the nearest to the school? Explain your thinking. |
Order from smallest to largest. Explain your reasoning:
|
Post Lesson Reflection
Lesson_________________
1) Number of class periods allocated to this lesson: ______________
2) Student Pages used: __________________
3) Adaptations made to lesson: (For example: added extra
examples, eliminated
certain problems, changed fractions used)
4) Adaptations made on Student Pages:
5) To improve the lesson I suggest:
| Prev | Next |