OLUTION OF MATH 307 MIDTERM 1

Note that for solutions of numbers 3 (a), (b), and 4, 5, I gave necessary hints
for you only, not the complete solutions as students should show in their work.

1. The Mathematical Induction
(a) (4 points) Use the mathematical induction to prove the formula:

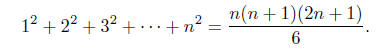
Solution. For n = 1 : 1² = 1, and 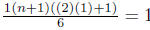, correct.
Assume that the formula is correct for n = k ≥ 1, that means for this k,

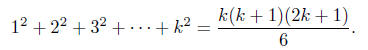
Now we prove the formula for n = k + 1. Consider 1² + 2² + 3² + · · · + k² + (k +
1)²
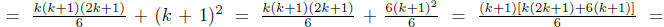
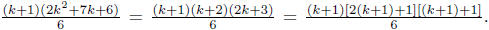Compare with the given
formula we see that it is correct for n = k + 1. Hence the formula is proved.

(b) (5 points) Use the mathematical induction to prove that for n > 0, 15 is a
divisor of ().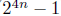

Solution. For n = 1,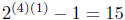, and 15|15, correct.
Assume that the statement is correct for n = k ≥ 1, that means 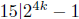. For
n = k+1 we see
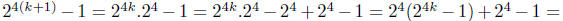
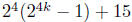. But by our induction assumption, 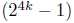is divisible by 15. Hence
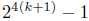is divisible by 15. The proof is complete.

2. The Binomial Theorem
(a) (3 points) Write the binomial formula: (a + b)ⁿ
Solution.

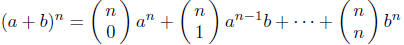
(b) (4 points) Prove that

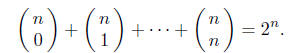
Solution. Using (a) for a = b = 1.

3. Prime numbers
(a) (5 points) Let n > 1 be an integer. Prove that 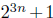is not a prime number.
Hint:

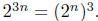
Solution: 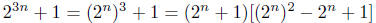for n > 1 we see each
factor is greater than 1. Hence 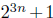is NOT prime.

(b) (4 points) Show that for any integer n > 1, n⁵ + 1 is not a prime number.

Solution. Use the formula n⁵ + 1 = (n + 1)(n⁴ − n³ + n² − n + 1). For n > 1
each factor is greater than 1.

(c) (6 points) Let p be a prime number. Find all values of p such that 5p + 1 is
a perfect square .

Solution. Since 5p + 1 is a pefect square, 5p + 1 = a² for some positive integer
a. Hence 5p = a² − 1 = (a − 1)(a + 1). Therefore 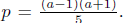Now, since 5 is a
prime, we must have either 5|(a − 1) or 5|(a + 1). This together with the fact that p is
a prime gives either a − 1 = 5 or a + 1 = 5. The first case yields a = 5 + 1 = 6 and so
p = 7. The second case gives a = 5− 1 = 4, and so p = 3.
Answer: p = 7 or p = 3.

Remark. From the previous part (c), we can state a general problem: Let q, p
be prime numbers such that qp+1 is a perfect square. Find q and p. Using the solution
of (c) above, you can try to answer this problem. A list of such q, p less than 106 was
found today (4/27) by my younger son (an undergraduate computer science student
at HTC, OU). There are 78498 prime numbers in the range [2, 1000000] in which 8169
prime-pairs that satisfy the condition pq + 1 = n². View attachment for details.

4. Greatest common divisor (gcd) and least common multiple (lcm)
(a) (4 points) Find gcd and lcm of 2030, and 4246.

Solution. Use Euclidian algorithm, or write these numbers in the product of
primes to find the answers for gcd. For lcm use the formula

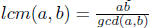
(b) (5 points) Find x and y such that gcd(48, 138) = 48x + 138y.

Solution. Use Euclidian Algorithm. Answer: x = 3, y = −1

5. Linear Diophantine Equations
Find the general solution of the following equations:
(a) (5 points) 24x + 36y = 156.

Solution. Use Euclidian Algorithm to find gcd(36, 24) = 12 and a specific
solution x₀ = −13, y₀ = 13. Then the general solution is:
x = −13 + 3t, y = 13 − 2t for any t ∈R.

(b) (5 points) 102x + 1003y = 221.

Solution. Do the same way as part (a). Answer: x₀ = 130, y₀ = −13,
gcd(102, 1003) = 17. Hence the general solution is: x = 130 + 59t, y = −13 − 6t
for all t ∈R.