Sqrt(2) is Irrational

The standard proof that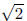 is irrational, which appears both in Rudin and on
Wikipedia, is (or can be written as) a reductio ad absurdum (RAA): if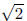 is rational
then it cannot be expressed as a reduced form ( with all common factors divided out);
since any actual rational number can be expressed in reduced form, it must be
that 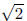is not rational. More succinctly: if 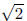is rational then it both has and does not
have a reduced form representation.

Below, I give a version of the standard proof. My version is somewhat longer
than the usual versions because I take care to spell out the RAA logic . I also
give a second proof, a contraposition, that takes the central idea, that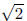cannot
be expressed in reduced form, and presents it in a way that does not require first
assuming that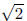 is rational. Both proofs are correct. Which proof you prefer is
largely a matter of taste. I prefer the second, less standard version; the argument
seems more straightforward to me, despite the fact that it relies on a construction
that may at first seem abstract.

Theorem 1.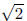 is not rational.

Proof. I give two proofs , the first is a form of reductio ad absurdum, the second a
contraposition.
1. First Proof. Suppose that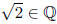

Then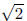can be expressed as a ratio of natural numbers. Consider any such
representation: a, b∈ N such that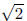 = a/b. Therefore a² = 2b². In particular,
 a² is even. It is a theorem of number theory that this implies that a must
also be even, hence there is a ∈ N such that 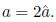Hence 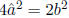, which
implies 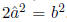. The same argument, now applied to b, gives a 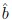∈ N such
that b = 2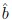, hence 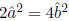² or

:
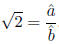
Since = a/2 and 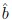= b/2, this implies that a=b is not in reduced form. Since
a/b was an arbitrary ratio representation of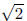, this implies that there is no
ratio representation of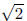 in reduced form.

On the other hand, it is a theorem of number theory that any ratio of natural
numbers can be put into reduced form.

Therefore, the hypothesis that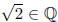 implies that 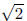both can and cannot
be represented as a reduced form ratio of natural numbers. The conclusion
that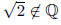follows by RAA.

2. Consider any set 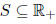with the following properties .
(a) There is an a, b∈ S such that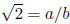
(b) If p, q ∈ S and p² = 2q then there is a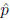 ∈ S such that p = 2.

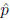This definition is not vacuous. For example, take S = R+.

Consider any a, b ∈ S such that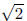 = a/b. Then a, b ≠ 0. Since 2b² = a², the
construction of S implies that there is an a₁ ∈ S such that a = 2a₁. Hence
, or b² = 2a². Again by construction of S, there is a b₁ ∈ S such
that b = 2b₁, hence 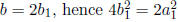or

:
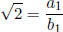
Continuing in this way yields sequences {a_t },  { b_t } such that for all t, a_t /  b_t  =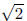
 and for t large enough, a_t, b_t < 1. Since a_t, b_t ≠ 0, this implies a_t, b_t ∈ N.
Thus S ≠ N.

Since S was arbitrary, this shows that N does not satisfy the two criteria
above: it fails either the first or the second (or both). It is a basic result in
number theory that N satisfies the second condition (this was already invoked
in the previous proof ). Therefore it follows that N violates the first, which is
equivalent to saying that

Remark 1. Essentially the same argument shows that for any natural number n,
either n is the square of another natural number or
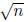is irrational.