INTEGER AND RATIONAL NUMBERS

Theorem 7.7 The ordering of rational numbers is well defined.

Proof Let [x, y] = [a, b], [z,w] = [c, d], and [x, y] < [z,w] with b, d, y, w >
0. We thus have

Hence the ordering is well defined.

We define addition and multiplication as follows,

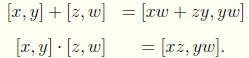
Theorem 7.8 Addition and multiplication of rational numbers are well
defined.

Proof Let [x, y] = [a, b] and [z,w] = [c, d].

For addition we have

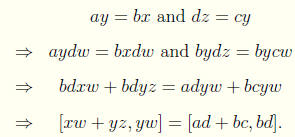
Hence addition is well defined.

For multiplication we have

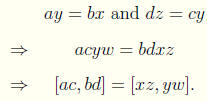
Hence multiplication is well defined.

Just as there is a natural embedding of the natural numbers into the
integers, there is the natural embedding of the integers into the rational
numbers given by the injection,



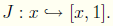
It is easy to verify that this injection is an embedding.

A Field

We leave it the reader to verify the following properties of Q .

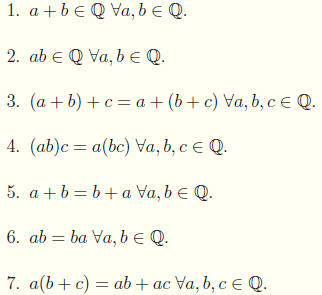
8. 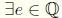such that a + e = e + a =

9. 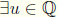such that au = ua =

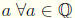
10. 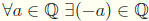such that a + (-a) = (-a) + a = 0

11. 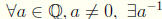such that aa^-1 = a^-1a = 1

The first 10 properties are identical to the properties of an Integral Domain.
Property 11* is replaced by property 11 where a^-1 is called the multiplicative
inverse, or reciprocal .

Any set with two binary operations satisfying these 11 properties is called
a Field.

Exercise Show that every field is an integral domain. That is to say, every
field has no zero divisors .

Differences and Quotients

Definition The difference between integers or rational numbers a and b
is a + (-b), which is written a - b.

Definition The quotient of two rational numbers a and b is a · b^-1, which
is written .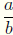

We can see that difference and quotient can be regarded as a binary oper-
ations, we also notice that neither operation is commutative nor associative.
Exercise For any two rational numbers p < q, show that .

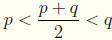Exercise Show that

1. If p, q, r are rational numbers where p ≤ q and r > 0, then pr ≤ qr.

2. If p, q, r are rational numbers where p ≤ q and r < 0, then pr ≥ qr.

3. If p and q are positive rational numbers, then :

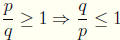Mathematical Induction

The next theorem is a special case of transfinite induction, that is widely
used in many situations. Before we state and prove the theorem we need two
small lemmas that we present as exercises .

Exercise 1. Define the map Ø : N → 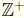by Ø(a) = [a + 1, 0]. Show that

Ø(a) + 1 = Ø(a + 1).

Exercise 2. Show that 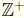is order isomorphic to ω.

Theorem 7.9 The Principle of Mathematical Induction If 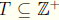 such
that the fol lowing conditions are true:

i. 1 ∈ T

ii. if k ∈ T, then k + 1 ∈ T,

then T = .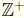

Proof Consider the order preserving bijection Ø : ω → 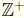defined by
Ø(a) = [a + 1, 0]. Let A = Ø^-1(T). Let x ∈ ω such that S(x) 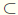A.

If x = 0, then Ø(x) = 1 ∈ T => x ∈ A. If x ≠ 0, then

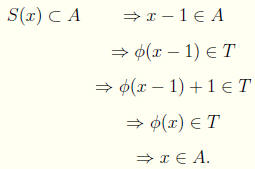
Thus by Transfinite Induction .

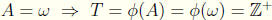The Cardinality of Integers and Rational Numbers