HINTS ON MATH 102 HOMEWORK 8

8.1 (or Handout 3, Section 4) would help. This is indeed the easy case: you
can just plug formula and you are done.

(7)

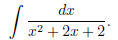
You have seen this already. You cannot factorize x² + 2x + 2 because
the discriminant is negative (if you know what that is). In any case you
will know that this is something that you cannot factorize, and you try
completing the square : you get

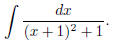
So if you now make the change of variable u = x + 1, you end up with the
integral

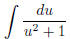
which you can evaluate by a formula. So the answer is just

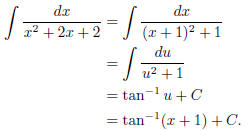
(8) Try now

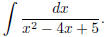
(9) However, some times in the denominator you run into a product of quadratic
expressions that you cannot factorize, with some other say linear factors .
e.g.

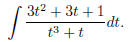
Here things gets a little complicated, but not too much: you just have to
realize two things . First, you still want to factorize the denominator as
much as possible. So you get

t³ + t = t(t² + 1).

If t² + 1 could be further factorized, you should indeed factorize it and use
partial fraction, but since it actually couldn\'t be factorized, the best you
can do is to do partial fraction from here. So the second thing that you
need to know is that the partial fraction that you will get will be of the
form

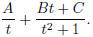
In other words, on the top of t²+1, you get not only a number , but a linear
factor in t, namely Bt + C. As long as you pick a partial fraction of this
form you will be able to compute the partial fraction decomposition:

Let

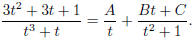
Then the right hand side is equal to

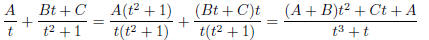
so comparing coefficients, we get

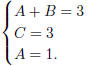
This says A = 1, B = 2 and C = 3, so

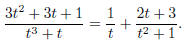
You want to integrate the right hand side here, and the first term is alright;
you know how to integrate 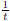. The trouble comes with the second term.
However, this is not very hard: recall from Section 8.1 (or Handout 3,
Section 4) that there are some basic integrals that you can evaluate. One
of them is

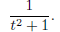
There is a formula for that. Another one is

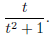
You can do this by substitution . So all in all, to compute the integral

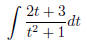
it suffices to split the integral into the sum of two terms : just do

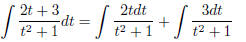
and evaluate each of them separately. Together, we get

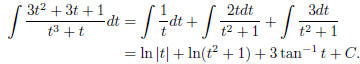
(10) Try now

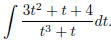
(11) Finally, sometimes you run into a rational function in which the degree of
the polynomial on the numerator is bigger than or equal to the degree of
the polynomial on the denominator. In this case, you just need to do one
extra step: Always perform a long division first to simplify the fraction into
a sum of a polynomial with another rational function whose numerator has
degree smaller than the degree of the denominator. This is really like if
you have a fraction of numbers 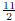you really want to write this as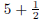
- you want to split out the `integral part\' of the fraction because it makes
the fraction more transparent and easier to deal with. Let\'s go through the
fol lowing (last) example together:

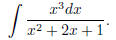
First, the power of the numerator is bigger than that of the denominator.
So we want to do a long division: we want to divide x³ by x²+2x+1. Step
back and take a look at the webpage I posted on line if you are not sure how
to do this. This is really easier than you might have thought; it is almost
like how you carry out a long division of numbers. The answer in this case
is the following: the quotient is x − 2, the remainder is 3x + 2. Hence

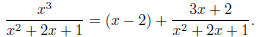
(Think about 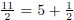: it is just another way of saying that when you
divide 11 by 2, you get a quotient of 5 and a remainder of 1.)

Now we want to integrate this fraction. The first term x−2, which does
not involve a quotient, is of course easy to integrate; we just get

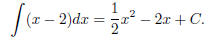
Do you see now why we want to split this `integral bit\' out now?

The second term is just slightly harder: you just want to repeat what
you have done so far when you integrate the other proper fractions above.
Here is how you do it:

First step: factorize the denominator as far as possible. Here this means
you write x² + 2x + 1 = (x + 1)².

Second step: decompose

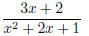
into a partial fraction. Now we have a repeated linear factor in the denom-
inator! So we would find the partial fraction decomposition by letting

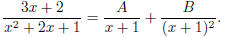
Then the right hand side is

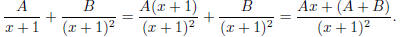
Comparing coefficients, we get

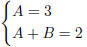
so A = 3, B = −1. In other words,

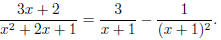
Integrating, we get

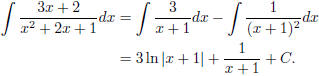
Together with the easy term, we get

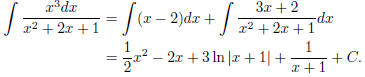
Just a final quick tips: your remainder will always have degree strictly
smaller than your denominator.

(12) Try now

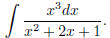
Hope this helps you a little bit when you work on your homework this week!
P.S. Can you summarize, in your own words, what you have learned from the above
examples?