Systems of Equations
Topic 2‐1 Systems of Equations
A system of equations is a collection of two or more
equations with the same solution set . The
equations are simultaneously satisfied .
A solution to a system of equations should contain
values for each variable that solve each equation in
the system.
We will be focusing on systems of two linear
equations.
Henceforth, our solutions will be ordered pairs .
Are the ordered pairs (3, 1) and (1, 2) solutions to
the following system of equations?
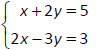
We will cover 3 ways of solving a system of
equations.
1. finding the intersection point on the graphs of
the equation
2. applying the substitution method
3. applying the elimination method (also known as
the addition method )
Solve the system of equations by finding the point
of intersection, if one exists.
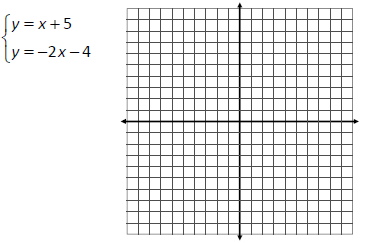
Solve the system of equations by finding the point
of intersection, if one exists.
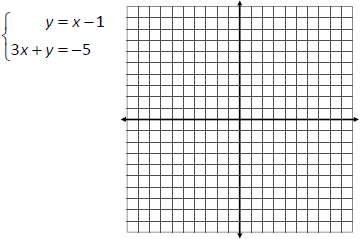
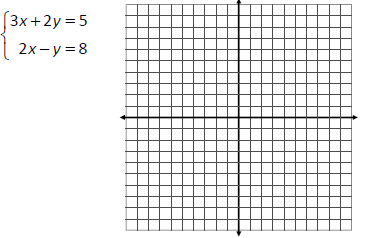
Solve the system of equations by finding the point
of intersection, if one exists.
Consistency ‐ property of having a solution
Independence ‐ property of having uniqueness
Most systems of linear equations are consistent and
independent. That is, they have a solution and are
not a collection of the same line. With a consistent
and independent system there is exactly one
solution which occurs at an intersection point.
Some systems of linear equations are inconsistent.
That is, the two equations never intersect and thus
have no solution. Graphically, these lines must be
parallel and unique.
Some systems of linear equations are dependent.
That is, the two equations are really one equation
producing one line. These systems have infinitely-many
solutions along the common line . Graphically,
these lines are coincident.
Solve the system of equations by finding the point
of intersection, if one exists. If the system has
infinitely‐many solutions or it has no solutions, state
as such.
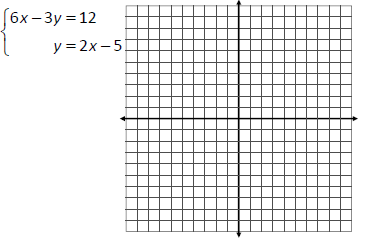
Solve the system of equations by finding the point
of intersection, if one exists. If the system has
infinitely‐many solutions or it has no solutions, state
as such.
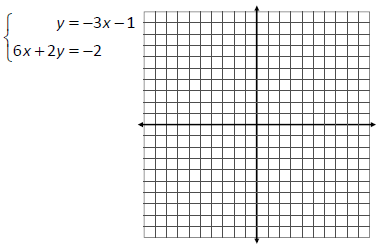
Topic 2‐2 Solving Systems: Substitution Method
With the substitution and elimination methods, the
goal will be to take systems with multiple equations
and multiple variables and merge them into a single
equation involving a single variable.
Substitution Method for Solving Systems of
Equations
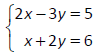 |
1. Solve either equation for x or y. 2. Plug that equation in for the variable in the other equation. 3. Solve the created equation involving one variable. 4. Plug the solution found in step 3 into any equation involving two variables & solve. 5. Write your solution as an ordered pair. |
Solve and classify the system of equations.
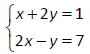
Solve and classify the system of equations.
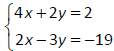
Solve and classify the system of equations.
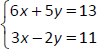
Solving systems of linear equations by the
substitution method or the elimination method
works obviously when the system is consistent and
independent.
To recognize when the system is inconsistent
(having no solutions) or dependent (having
infinitely‐many solutions along a common line), look
for systems which do not produce unique solutions:
An inconsistent system should produce a
contradiction when the equations are merged.
A dependent system should produce an identity
statement when the equations are merged.
Solve and classify the system of equations. If the
system has no solutions or infinitely‐many
solutions, state that.
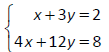
Solve and classify the system of equations. If the
system has no solutions or infinitely‐many
solutions, state that.
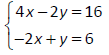
| Prev | Next |