Direct Proof
Ex. Give a direct proof of the following:
For every integer n, if n is odd then n^2 is odd.
Proof:
Let n be an odd integer.
Then n = 2k + 1 for some integer k.
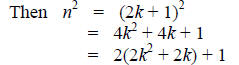
Therefore, n^2 is odd.
Ex. Give a direct proof of the following:
If r and s are rational numbers then r + s is a rational number .
Proof:
Let r and s be rational numbers.
Then r = a⁄b and s = c⁄d for some integers a, b, c, d with b ≠ 0 and d ≠ 0.
We then have
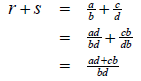
Note that ad+cb is an integer and bd is a non zero integer .
Therefore r + s is a rational number.
Ex. Give an indirect proof of the following:
For every integer n, if n^2 is odd then n is odd.
Proof:
We will show ( n^2 is odd -> n is odd ) indirectly by showing ( n is even -> n^2
is even ).
We want to prove that if n is not odd, then n^2 is not odd.
Let n be an even integer.
Then n = 2k for some integer k.
Then
n^2 = 4k^2
= 2(2k^2)
Thus n^2 is an even integer.
Proof by Contradiction
Ex. Give a proof by contradiction of the following:
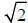 is irrational.
is irrational.
Proof:
Suppose that 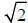 is not
irrational (suppose it is rational).
is not
irrational (suppose it is rational).
Then 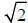 =a/b for some integers a and b.
=a/b for some integers a and b.
Without loss of generality we can as sume that a/b is in reduced form ,
that is we can assume that a and b share no common divisor .
Square both sides to obtain
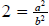 .
.
Then
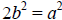 .
.
We now can see that 2 divides a ^2.
This implies that 2 divides a.
This implies that 4 divides a^2.
So, we can write a^2 as 4q for some integer q.
Our equation 2b^2 = a2 now becomes 2b^2 = 4q.
Thus b^2 = 2q.
So, 2 divides b^2.
Thus 2 divides b.
This is a contradiction. We assumed that
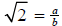 where a and b share no common divisor, yet we have arrived at the fact that a
and b must both be divisible by 2.
where a and b share no common divisor, yet we have arrived at the fact that a
and b must both be divisible by 2.
Therefore our assumption that
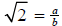 cannot be correct.
cannot be correct. 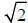 cannot be a rational
number. Hence
cannot be a rational
number. Hence 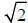 is irrational.
is irrational.
Proving “if and only if” statements
Ex. Prove that r is a rational number if and only if 2r is a rational number.
Proof:
(->)
First we shall show that if r is a rational number then 2r is a rational number.
Let r be a rational number.
Write r as a⁄b with a and b integers, b ≠ 0.
Then 2r = 2a⁄b . Since 2a and b are integers and b ≠ 0, we see that 2r is a
rational number
(<-)
Next we shall show that if 2r is a rational number then r is a rational number.
Let 2r be a rational number.
Write 2r as a⁄b with a and b integers, b ≠ 0.
Then r = a⁄2b . Since a and 2b are integers and 2b ≠ 0, we see that r is a
rational number.
We have now proved that r is rational iff 2r is rational.
Proving Statements are Equivalent
Ex. Show that the fol lowing are equivalent :
p1 : n is an even integer
p2 : n + 1 is an odd integer
p3 : n^2 is an even integer
Proof:
p1->p2
Suppose n is even. Then n = 2k for some integer k.
Then n + 1 = 2k + 1.
Thus n + 1 is odd.
p2->p3
Suppose n + 1 is odd. Then n + 1 = 2k + 1 for some integer k.
Then n = 2k.
Thus n^2 = 4k^2 = 2(2k^2).
Therefore n^2 is even.
p3->p1
We will show that n^2 is even -> n is even by an indirect proof (n is odd -> n^2
is odd).
Let n be an odd integer. Then n = 2k + 1 for some integer k.
Then n^2 = (2k + 1)^2 = 4k^2 + 4k + 1 = 2(2k^2 + 2k) + 1.
Thus, n^2 is odd.
We have now verified that these three propositions are equivalent.
Proof by Cases
Ex. Prove that the square of an integer ends with 0, 1, 4, 5, 6, or 9.
Proof:
Let n be an integer which ends in b. We can write n as follows: n = 10a + b.
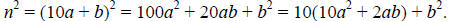
The last digit in the decimal expansion of n^2 is completely de termined by b ^2.
We need to examine b^2 for each possible value of b .
If b = 0 then b^2 = 0.
In this case the last digit of the decimal expansion of n^2 is 0.
If b = 1 or b = 9 then b^2 = 1 or b^2 = 81.
In either case the last digit of the decimal expansion of n^2 is 1.
If b = 2 or b = 8 then b^2 = 4 or b^2 = 64.
In either case the last digit of the decimal expansion of n^2 is 4.
If b = 3 or b = 7 then b^2 = 9 or b^2 = 49.
In either case the last digit of the decimal expansion of n^2 is 9.
If b = 4 or b = 6 then b^2 = 16 or b^2 = 36.
In either case the last digit of the decimal expansion of n^2 is 6.
If b = 5 then b^2 = 25.
In this case the last digit of the decimal expansion of n^2 is 25.
Thus, the last digit of n^2 must be either 0, 1, 4, 5, 6, or 9.
Existence Proofs
Ex. Use a constructive proof to show that there exists irrational numbers x and y such that x + y is rational
Proof:
Consider the irrational numbers
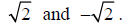
Note that
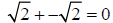 , and 0 is a rational number.
, and 0 is a rational number.
Ex. Use a nonconstructive proof to show that there exists irrational numbers x and y such that xy is rational.
Proof:
Consider 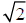 , which has been shown to be
irrational.
, which has been shown to be
irrational.
If 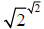 happens to be rational then we are d one .
happens to be rational then we are d one .
Suppose not, suppose 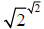 is irrational. Then
consider
is irrational. Then
consider 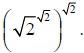
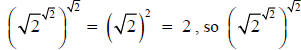 is rational.
is rational.
Ex. Prove that every odd integer is the difference of two perfect squares
Let n be an odd integer. Then n = 2k + 1 for some integer
k.
Note that
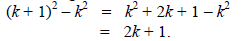
| Prev | Next |
