Math 099 Final Exam

Instructions: While you may use additional scratch paper for your own work, only the work shown in the sections of
this test will be considered for credit.

1 Simplify

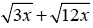
_____________ [2]

2 Simplify

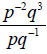
as much as possible

_____________ [2]
(only positive exponents )

3 Convert to radical notation:

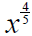
_____________ [2]

4 If f (x) = 3x - 4 then f (t +1) = ?

_____________ [2]
(simplified)

5 Combine

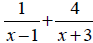
into a single fraction

_____________ [3]

6 Simplify

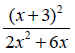
_____________ [3]

7 What is the slope m of a line that is perpendicular to the line x + 3y = 4 ?

m = _____________ [2]

8 Solve for y :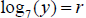(Your answer should involve r.)

y = _______________ [2]

9 Find all solutions: 3(x +1) = 2(4x +1) - 2

x = _____________ [3]

10 Find all solutions:

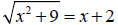
x = ___________________ [3]

11 Find all solutions:

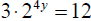
y = _____________ [2]

12 Find all solutions:

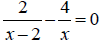
x =_____________ [3]

13 A friend kicks a ball high into the air, and it passes the top of the building after a certain number of seconds. If we double this number, then subtract 9, and then square the result, we get the number 25. After how many seconds did the ball pass the top? Give all possible solutions.

After ___________ seconds [3] (list all solutions separated by commas)

14 Solve by using the quadratic formula:

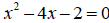
x = ____________ , ____________ [3] (list all solutions in simplified radical form)

15 Campbell’s is designing an improved soup can. The
radius of the top of this new can will be half its height.
In addition it must hold 25 cubic centimeters of soup.
What should the height of the can be?

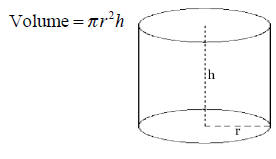
h = __________________ cm [3]
(rounded to the nearest hundredth)

16 Find all solutions to the equation 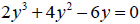by factoring . Show your work.

y = _______________________________ [3] (list all solutions, separated by commas)

17 Find the exact coordinates of the point at which the lines 5x + y =1 and x - 0.1y = 0.4 intersect.

(x, y) = ( , ) [3] (exact fractions)

18 The graph of F(x) is shown below.

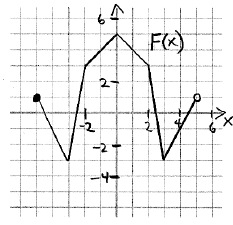
(a) F(2) =	______________ [1]
(b) The domain of F is	______________ [2]
(c) The range of F is	______________ [2]
(d) Find all solutions to F(x) = 4	______________ [2]
	(list all solutions, separated by commas)

19 The graph of 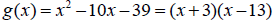is sketched very roughly below

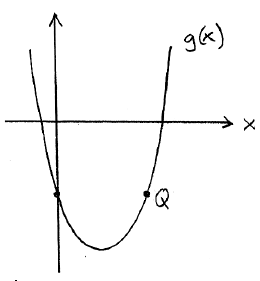
(a) Find the y-intercept	___________ [1] (x,y) coordinates
(b) Find the x-intercepts	__________________ [2] (give (x,y) coordinates of all intercepts )
(c) Find the (x, y) coordinates of the vertex	__________________ [2] (x,y) coordinates
(d) What are the (x, y) coordinates of the point Q?	__________________ [2] (x,y) coordinates

20 Consider the line that is parallel to 2x - 7y = 3 and passes through the point (3,0) .

(a) The slope of the line is:

m = ______________ [2]
(exact answer)

(b) The equation for the line is:

y = _____________________ [2]

21 You arrive at the gas station to fill your car up, but you don’t have enough money to fill it up all the way. The
number of gallons you can purchase is inversely proportional to the price per gallon of gas. (Another way of saying
the same thing is that the number of gallons you can purchase varies inversely with the price per gallon.) If the price
per gallon of gas is $3.12, then you can afford 5.5 gallons. How many gallons can you afford if you decide to upgrade
to premium gas, which costs $3.39 per gallon?

You can afford ____________ gallons of premium [5]
(round to two places after the decimal)

22 A farmer needs a new pair of identical rectangular pens for her pigs. She will
build the two pens so that they share a side to save materials. If the dimensions of
each pen are labeled x and y, then the pens look like the figure to the right when they
are viewed from above.

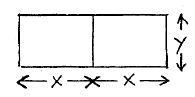
a) Write an equation that relates the combined area of the two pens to the dimensions x and y.

_________________________ [2]

b) The farmer only has 70 meters of fencing, and she wishes to use it all. Write an equation involving x and y that
expresses the fact that all of the fencing will be used.

__________________________ [2]

c) If the farmer wants to make the pens with the greatest combined area using all of her 70 meters of fencing, what
should the dimensions x and y be? Solve for x and y algebraically, and show your work.

Area is greatest when
x = ____________ meters
and
y = ____________ meters [4]
(round to the nearest tenth)

d) If the farmer makes the dimension x too large, then the combined area of the pens will become small. For what
positive x dimension does the combined area of the pens become zero .

Area = 0 when x = ____________ meters [2]
(round to the nearest tenth)

23 While at the county fair you find that you have lost your cell phone. According to the map, the lost-and-found is
located 200 meters north and 350 meters east of the information desk. Also according to the map, your current
location is 180 meters south and 55 meters east of the information desk.

a) How far are you from the lost-and-found?

You are ____________ meters from the lost-and-found. [3]
(round to the nearest tenth)

b) If you walk at 3 meters per second, how long will it take you to reach the lost-and-found at this rate, assuming you
can walk there in a straight line?

It will take you ____________ seconds to reach the lost-and-found. [2]
(round to the nearest tenth)

24 If you take a sheet of paper and fold it in half, your folded sheet will have twice the original thickness. If you
continue folding, the thickness doubles with each new fold. If N is the number of folds, and T is the resulting
thickness in meters, the relation between these two variables is given by the model

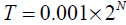
a) According to this equation, what is the thickness of the sheet of paper being used?

____________ meters [2]
(give three places after the decimal point )

b) According the model, how thick will the stack be after 11 folds?

__________ meters [2]
(give one place after the decimal point)

c) According to the model, after how many folds will the stack be one kilometer thick? (1 kilometer = 1000 meters)

__________ folds [4]
(round up to the next whole number)

25 You wish to rent a bike for most of a day, and there are two local businesses that offer bike rentals for up to 24 hours.

Abelian Bicycles charges $15 for a day rental plus $4.50 per hour of usage.
Bellevue Bicycles charges $17 for a day rental plus $4.25 per hour of usage.

After how many hours of usage does Bellevue Bicycle’s offer become a better deal?

After __________ hours. [5]

26 An elevator starts out on floor 1 of a building. At time
t = 0 it begins moving upward to floor 5, where it arrives
after 15 seconds. It spends 10 seconds on floor 5, and then
moves to floor 3, which takes 5 seconds of travel time. After
spending 10 seconds on floor 3, it moves up to floor 7,
which takes 15 seconds of travel time. The total trip from
floor 1 to floor 7 took 55 seconds.

Sketch the graph of the elevator’s height h above floor 0
(measured in floors) as a function of time t.

27 Bonus question [5 extra credit points] A house has an automatic thermostat that can maintain a fairly constant
temperature inside when it is turned on. The owner turns off the heat when he leaves the house. The temperature T of
the interior of the house on a winter day is graphed as a function of the number of hours t after the heat turned on at 6
a.m.

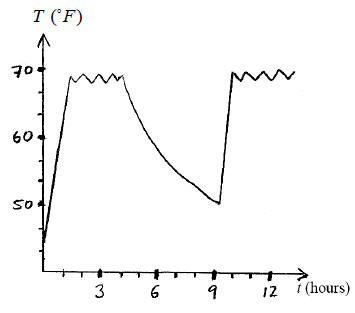
(a) During the time period shown, at about what time does the
owner leave the house? Give your answer in a form like “11:30” and
circle “a.m.” or “p.m.”

At _______________ a.m. / p.m. [1]
( circle one )

(b) After the owner leaves the house at the time in (a), about how
long does it take for the house interior to cool 10 degrees?

About ______________ hours [2]

(c) During the time period shown, for how many hours before noon
was the house’s interior temperature greater than 60 degrees

For ________________ hours before noon. [2]