Get it on Google Play Get it on Apple Store

Solving Equations

The goal of solving equations
When you are trying to solve an equation like:

x2 = 4,

you are trying to determine all of the numerical values of x that you could plug into that
equation. In this case, the numerical values that you could plug in are x = 2 and x = -2.

The numerical values that you find are called the solutions of the equation.

Some people find it helpful to interpret algebraic equations as verbal sentences in order to
remind themselves of what they are trying to accomplish. Some examples are given in
Table F.1 below.

Algebraic equation Equivalent sentence Solution(s)
x2 = 4 “What number, when you square them , give you
4?”		 x = 2, x = -2.
x + 2 = 8 “What number, when you add 2 to it, gives you
8?”		 x = 6.
2x = 16 “What power of 2 gives you 16?” x = 4.
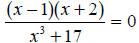“What numbers, when you plug them into the
numerator , give you zero?”		 x = 1, x = -2.

Table F.1: Algebraic equations, equivalent sentences and solutions.

Solving linear equations

A linear equation is one that only involves x - there are no powers of x, no radicals involving
x, no fractions with x in the denominator .

Solving linear equations involves expanding any brackets, grouping like terms and
simplifying as much as possible.

Linear equations always have exactly one solution.

Example F.1

Solve the following equations to find x.

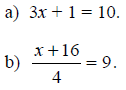
c) y = m×x + b.

Solution:

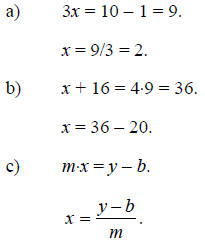
The working in part (c) involves the important assumption that m is not equal to zero.

Solving quadratic equations

Quadratic equations are equations that involve only x2, x and constants. Quadratic equations
may have one, two or no solutions.

Quadratic equations can be solved by factoring.

Example F.2

Find all solutions of the following quadratic equations. If you find less than two solutions,
explain how you know that you have found all of the possible solutions of the quadratic
equation.

a) x2 + 4x + 4 = 0.
b) x2 + 9x = -18.
c) 3x2 + x = -2.

Solution:
a) The left hand side of this quadratic expression is a perfect square,
(x + 2)2 = (x + 2)(x + 2) = 0.
To find the values of x that can be plugged in, ask yourself, “What values of x should I plug
in to make each factor equal to zero?” In this case, there is only one possible value of x,
namely x = -2.

b) The first step here is to get all of the non- zero terms on the left hand side of the
equation:

x2 + 9x + 18 = 0.

The left hand side can now be factored and analyzed in the same was as Part (a). Factoring
the left hand side of the quadratic equation:

(x + 6)(x + 3) = 0.

The values of x that can be plugged in to make the factors equal to zero are x = -6 and x =
-3. This quadratic equation has two solutions.

c) Proceeding in the same fashion as Part (b):

3x2 + x + 2 = 0.

This quadratic cannot be factored. You can verify this by calculating the quantity b2 - 4ac:

b2 - 4ac = 1 - 4×3×2 = -23.

Since this is negative, the quadratic expression 3x2 + x + 2 cannot be factored. Because
there are no factors, the quadratic equation:

3x2 + x + 2 = 0

has no real number solutions.

Solving power and radical equations

Power equations are equations involving only a single power of x and constants. For
example,

x2 = 4 + 0.5x2

is a power equation, because it involves only a single power of x (in this case, the power is
x2) and constants.

An equation like

x2 + 2x = 9

is not a power equation because it involves more than one power of x (this equation involves
x = x1 and x2).

Radical equations are like power equations, except that in a radical equation, the power of x
can be a fraction.

Solving power and radical equations is an application of the laws of exponents (see
Appendix A):

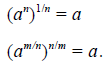
Example F.3

Find solutions of the following equations. If you are unable to find any solutions explain
why it is mathematically impossible to find real numbers that satisfy the given equation.

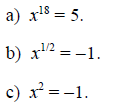
Solution
a) Applying the laws of exponents to both sides of the equation:

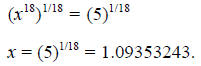
b) Applying the laws of exponents to both sides of the equation, and noting that

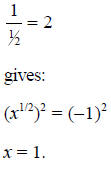
c) This equation has no real numbers x that can be plugged in to it. One way to see this is
to convert the algebraic statement of the equation into a verbal sentence. In this case, the
sentence might be something like, “What number, when squared, gives negative one?”
Since squares are always greater than or equal to zero, it is impossible to find a real number
that is negative when you square it.

Solving equations involving fractions

The usual strategy for solving involving fractions is to get rid of the fraction by finding a
least common denominator and then multiplying all terms by this common denominator.
This will convert the equation involving fractions to one of the other types of equations.

Not every equation involving fractions will have a solution.

Example F.4
Find the solutions of the following equations.

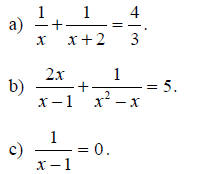
Solution:
a) There are three fractions in this equation. Since the strategy is to try to find a common
denominator, and then multiply all of the terms by this common denominator. In order to
find the common denominator it is only strictly necessary to take notice of the fractions with
x in the denominator. However, you can find a common denominator for all of the fractions
in the equation and still solve the equation correctly. Both ways of working this problem
are shown below.

Using the common denominator of

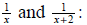
The common denominator here is x(x + 2). Multiplying all of the terms in this equation by
this common denominator gives:

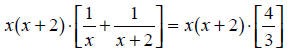Multiply by the common denominator.
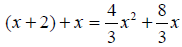Expand the brackets.
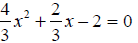Collect like terms.
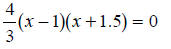Solve the quadratic by factoring.
x = 1, x = -1.5. The solutions of

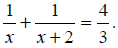Using the common denominator of all three fractions:
The common denominator here is 3x(x + 2). Multiplying all of the terms in this equation
by the common denominator gives:

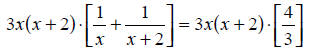Multiply by the common denominator.
3(x + 2) + 3x = 4x(x + 2) Expand the brackets.
4x2 + 2x - 6 = 0 Collect like terms.
4(x - 1)(x + 1.5) = 0 Solve the quadratic by factoring.
x = 1, x = -1.5 . The solutions of

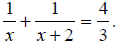b) There are several choices for the common denominator here. One of these choices is (x2
- x). This choice is the “least common denominator.”

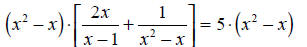Multiply by the common denominator
2x2 +1 = 5x2 - 5x Expand the brackets.
3x2 - 5x -1 = 0 Collect like terms.
3(x + 0.18046)(x - 1.847) = 0 Solve the quadratic by factoring.
x = -0.18046, x = 1.847 The solutions of

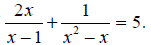You do not have to use the least common denominator when solving equations that involve
fractions - any common denominator will do. However, the least common denominator will
often lead to the simplest equation to solve after you have expanded the brackets and
collected like terms.

c) The common denominator here is (x - 1). Multiplying both sides of the equation by this
common denominator gives:

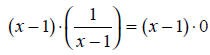Multiply by the common denominator.
1 = 0 Expand the brackets.

The last equation is quite perplexing, because one and zero are not equal. The significance
of this result can be understood by carefully examining the logic embodied in the working
here. We usually start the working by assuming that the equation has at least one solution,
and then proceed on this assumption with a series of algebraic manipulations designed to
find the numerical values of the solution(s). If we are able to find sensible numerical values,
then this confirms that the initial assumption (that there is at least one solution) is correct.
If, on the other hand, the algebraic manipulations lead to nonsense (like 1 = 0), then the
initial assumption (that there is at least one solution) must be flawed. That is, if the
algebraic manipulations lead to nonsense, then the equation does not have any solutions.

Solving exponential equations

Solving an exponential equation usually involves finding the value of an exponent (x in the
equation below) that will satisfy a given equation:

5x = 10.

It is important to remember that exponentiation and multiplication are not the same thing.
The solution to the equation 5x = 10 is x = 1.43067, not x = 2.

Solving exponential equations involves the use of the logarithm function. The logarithm
rule most useful for solving exponential equations is:

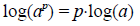
where a is a positive real number and p is any real number.

Natural logarithms (normally written “ln” instead of “log”) can also be used to solve
exponential equations. The working involved is basically identical, except that you write
“ln” instead of “log.”

Example F.5

Use logarithms to solve the exponential equation:
5x = 10.
Solution:
Applying logarithms to both sides of the equation:
log(5x) = log(10)
and using the law of logarithms to expand the left side:
x×log(5) = log(10).
All that remains is to make x the subject of the equation and evaluate the logarithms
numerically using a calculator:

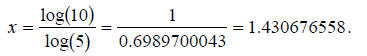
Example F.6

Carbon-14 is a radioactive isotope of carbon with a half life of 5730 years. The radioactive
decay of carbon-14 is used in biology and archaeology to establish the dates of ancient
relics. The mass, M, of carbon-14 remaining in a relic after T years is given by the formula:

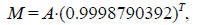
where A is the mass of carbon-14 in the relic when it was brand new.

The “mega-tooth” shark (Charcharodon megalodon) is an extinct, giant shark that
scientists think was about the size of a Greyhound bus. Much of what we know about this
shark comes from fossilized teeth that have been found in coastal regions of Virginia and
North Carolina. One fossil tooth found had about 0.0000001% of the carbon-14
remaining. How old is the tooth?

Solution:

The objective of this problem is to find a value for T. Since T appears in the exponent, this
will involve solving an exponential equation.

We are not told exactly how much carbon-14 is in the tooth in the beginning - that is, we are
not told A in this problem. However, we are told the relationship between M and A. In
symbols, this is:

M = 0.000000001×A.

Substituting this expression for M into the formula describing the decay of carbon-14 gives:

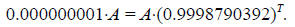
This equation has two unknowns, A and T. We want to find the value of T. Luckily, A
appears as a factor on both sides of the equation and can be canceled out:

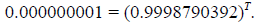
Applying logarithms to both sides of this equation, and rearranging to make T the subject of
the equation:

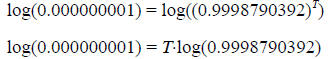
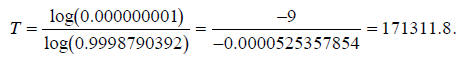
From this data, the “mega-tooth” appears to be about 171,000 years old.

Solving equations approximately using a graphing calculator

It is not very easy to solve some relatively straight-forward equations. For example, the
equation:

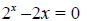
has two solutions: x = 1 and x = 2. However, none of the techniques for solving different
types of equations discussed in this appendix will help you to easily find these solutions.
In such a situation, the graphing calculator can be a useful tool for finding approximate
solutions to equations.

Example F.7
Find solutions for the equation:

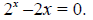
Solution:
In this situation, you can use a graphing calculator to try to find the solution(s) to this
equation by graphing the curve:

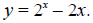
(See Figure F.1 below.) In trying to find the places where 2x -2x = 0, you are trying to
find the places where y = 2x -2x = 0. The places where y = 0 are the x-intercepts of the
curve y = 2x - 2x. From Figure F.1, the x-intercepts of y = 2x - 2x are located at x = 1 and x
= 2.

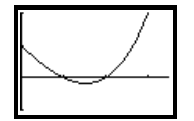
Window size: [0, 3.5]*[-1, 2]

Figure F.1: Finding solutions of 2x -2x = 0 using a graphing calculator.

Example F.8
Find approximate solutions for the equation:
2x -2x = 1.

Solution:
The working here follows a similar pattern to Example F.7 above. First, you use a graphing
calculator to plot a graph of y = 2x - 2x. This time, however, you are looking for the places
where y = 2x - 2x = 1, that is where the graph of y = 2x- 2x has height equal to one. Figure
F.2 (below) shows a plot of y = 2x - 2x along with a plot of a horizontal line of height 1.

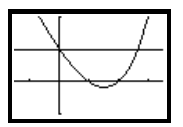
Window size: [-1.5, 3.5]*[-1, 2]

Figure F.2: Finding solutions of 2x -2x = 1 using a graphing calculator.

The x-values where the curve and the horizontal line intersect are the solutions of the
equation 2x -2x = 1. Using the TRACE or INTERSECTION functions of a graphing
calculator allows you to determine where these x-values are: x = 0 and x ≈ 2.659.

Note that the second solution (x ≈ 2.659) is not an exact solution of the equation. If you
plug 2.659 into the equation, you get:

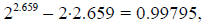
which is not precisely 1. The “solution” x ≈ 2.659 is a close approximation to the true
value of the solution.

Exercises for Appendix F
For Problems 1-10, find all of the solutions of the given equation.


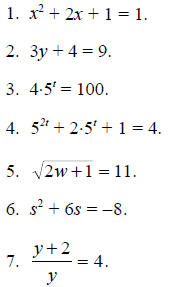
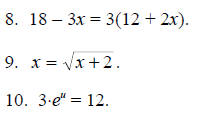
For Problems 11-20, solve the given equation for the variable indicated.

11. PV = nRT. Solve for T.
12. I = NeVA. Solve for e.

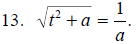Solve for t.

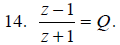Solve for z.

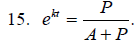Solve for P.

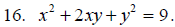Solve for y.

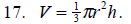Solve for h.

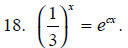Solve for c.

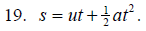Solve for u.

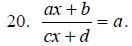Solve for x.

For Problems 21-25, use a calculator to find approximate solutions to the given equations.
How many solutions does each equation have?

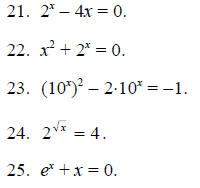
Answers to Exercises for Appendix F

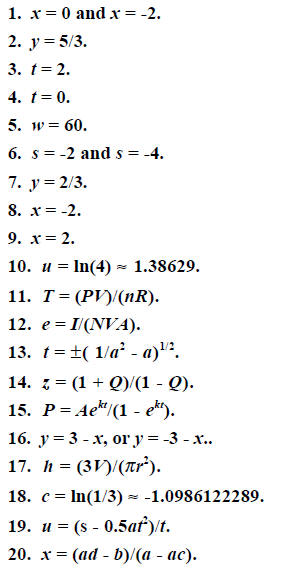
21. There are two solutions. One is located near x = -2.454386, and the other is
located near x = 4.8845.
22. There are no solutions of this equation.
23. There is only one solution: x = 0.
24. There is only one solution: x = 4.
25. There is only one solution, located near x = -0.5671433.

Prev Next