Dividing polynomials using long division

Algebrator can help you divide polynomials by using the long division method. Actually, it has a specific Wizard that can help you divide any two polynomials in one variable that you enter.

Take a look at what I did to solve your problem using Algebrator.

First, I opened the Long Division of Polynomials wizard and typed in the polynomials that you sent me in the input boxes provided:

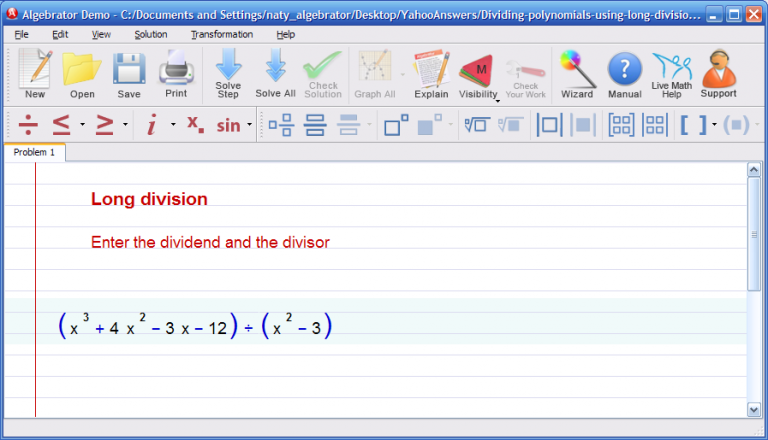
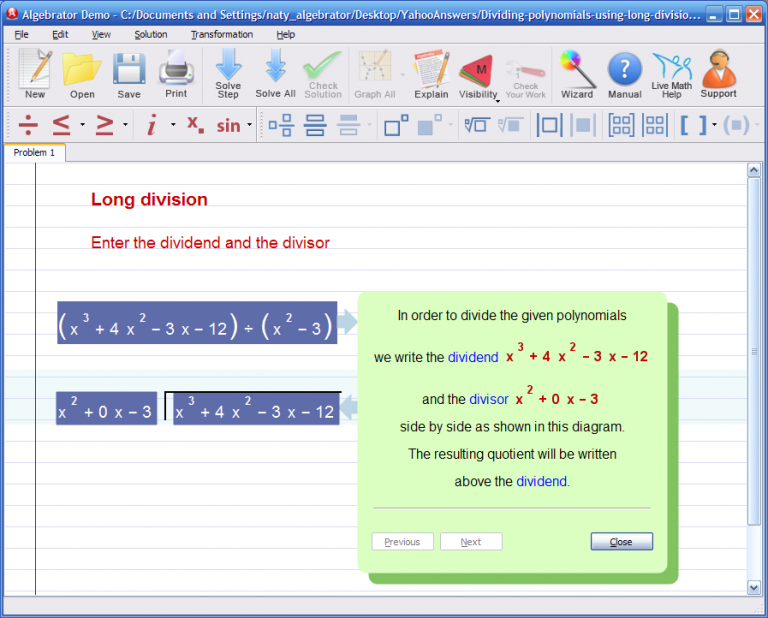
After entering the problem, I clicked on "Solve step" and the diagram showing the two polynomials involved in the long division showed. Clicking "Solve step" again showed me the first step of the solution process. Clicking on "Explain" showed me the explanation corresponding to that specific step, as shown in the image below:

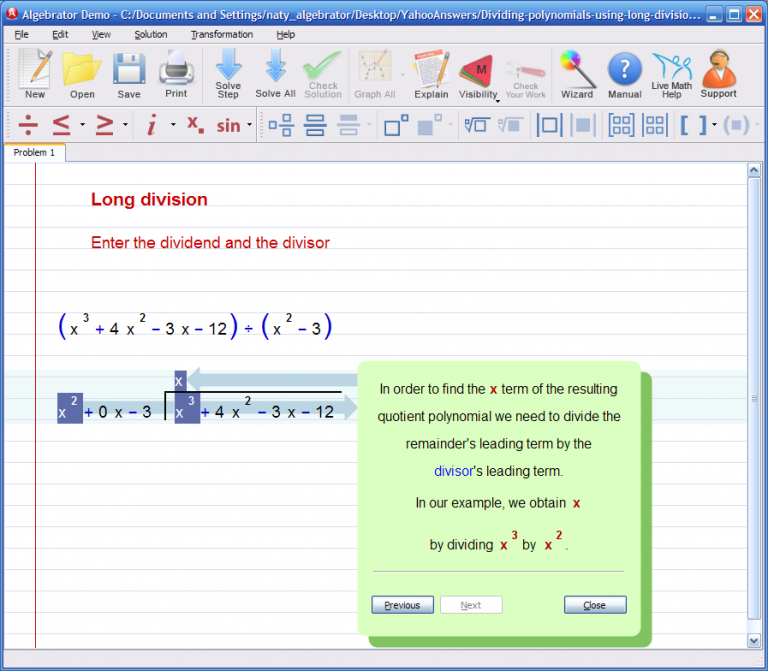
I clicked on "Solve step" again and the division process started. I clicked on "Explain" again and Algebrator showed me an explanation of how he obtained that 'x' in the quotient.

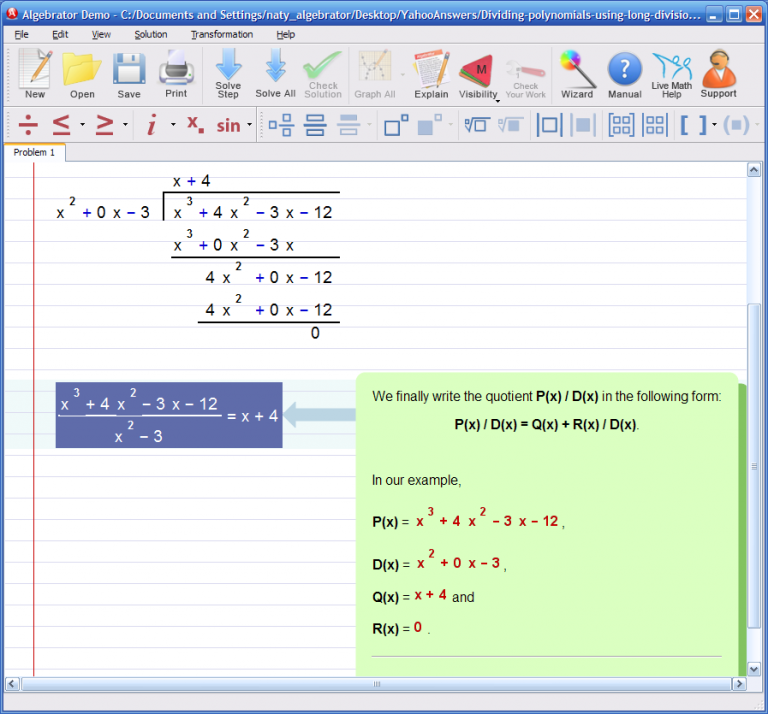
I went on clicking "Solve step" until the entire division process was finished. As you can see, the quotient was 'x + 4' and the remainder was '0'. That's what Algebrator showed me when I clicked "Explain" in the last line of the solution process.