Find the Equation of a Parabola using its Vertex and a Point
Original question text:
A parabola has vertex (4, 2) and contains the point (-2, 26).
What is the equation of the parabola?Option A: y = 2/3(x - 4)^2 + 2Option B: y = 7/9(x - 4)^2 + 2Option C: y = 4(x 4)2 + 2Option D: y = 6(x 4)2 + 2How can Algebrator help you with this problem?
Algebrator can easily solve problems such as the one you posted on Yahoo Answers.
Finding the Equation of a Parabola using its Vertex and a Point is one of the many tasks available on the Wizard menu.
An example using your equation is described below.
You must first start by entering the Vertex and the Point.
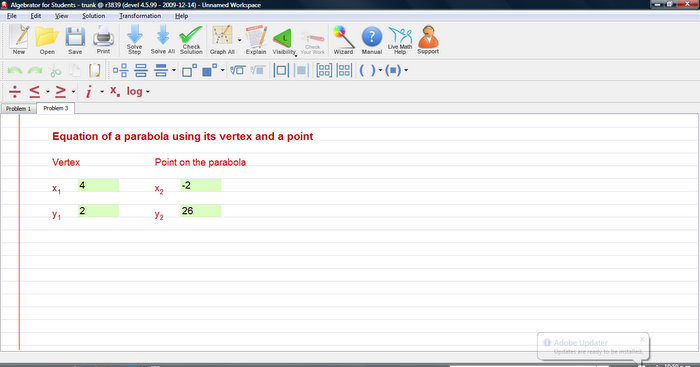
We will need to use the following formula:
Y = a(x-h)^2+k
An explanation can be obtained by clicking on the "Explain" button.
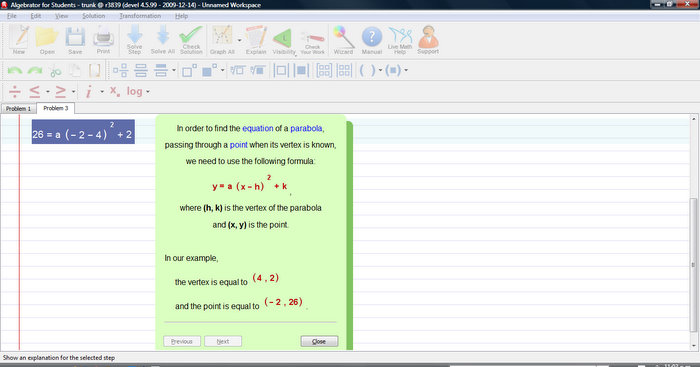
Some Important features are:
1.Flash demos, found under the drop-down menu "Help->Tutors".
The demos are also available online at "https://softmath.com/demos/", where you may simply select any of the ".htm"
files and the demo will play within your browser
2. Wizard button - for example, click the Wizard button and look under the category of "Parabola" to see the many useful
templates for Parabola equations.
3. The Explain button, which provides the mathematical logic involved in the selected step.
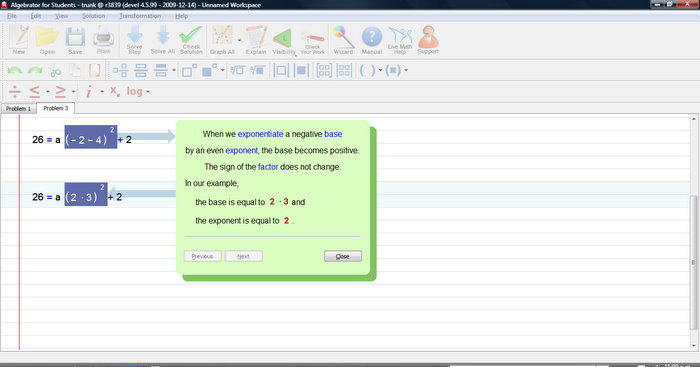
We need to distribute the exponent over each factor in the term.
The following rule is applied:
(AB)^c = A^c.B^C
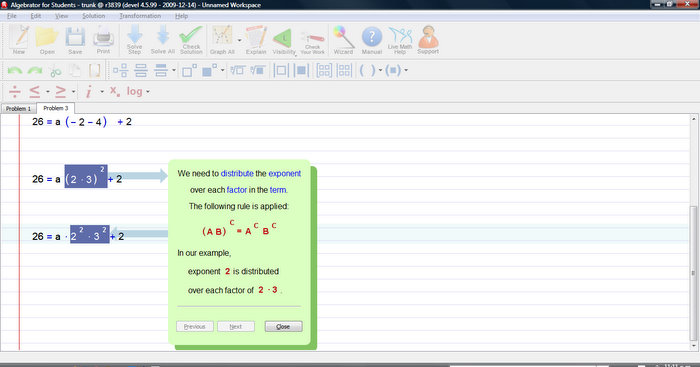
In order to solve this linear equation we need to group all the variable terms on one side, and all constant terms on the other.
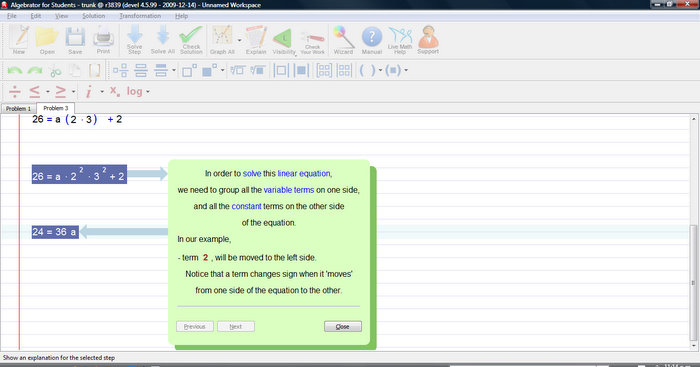
You can see the rest of the step-by-step solution process by clicking on the "solve step" button several times.
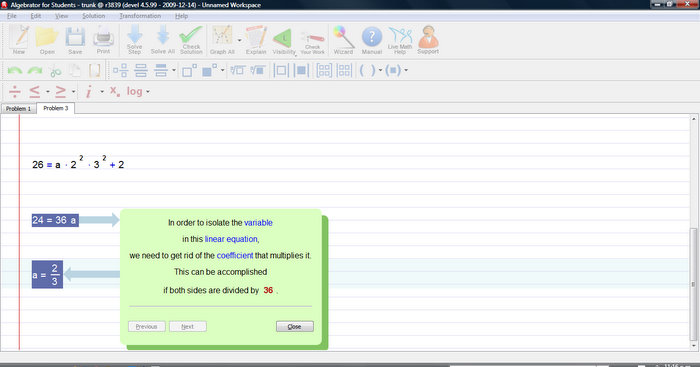
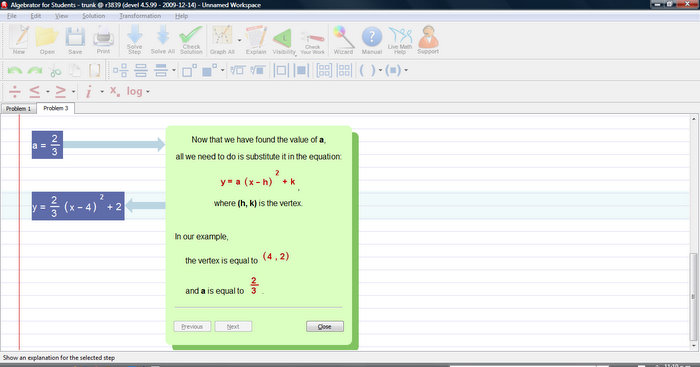
Now that we have found the value of a, all we need to do is substitute it in the equation:
y = a(x-h)^2+k
Vertex = (4,2)
a = 2/3
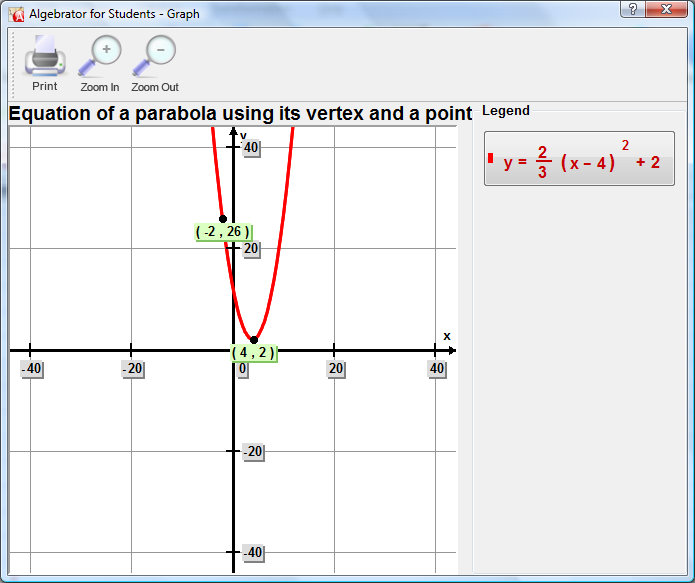
Finally you can also see the graphical representation of the solution.
| Prev | See Full List of Math Problems Explained in Detail | Next |

