Problema Solution
A farmer is going to divide her 40 acre farm between two crops. Seed for crop A costs $10 per acre. Seed for crop B costs $20 per acre. The farmer can spend at most $700 on seed.
If crop B brings in a profit of $60 per acre, and crop A brings in a profit of $70 per acre, how many acres of each crop should the farmer plant to maximize her profit?
Answer provided by our tutors
The restriction equations are:
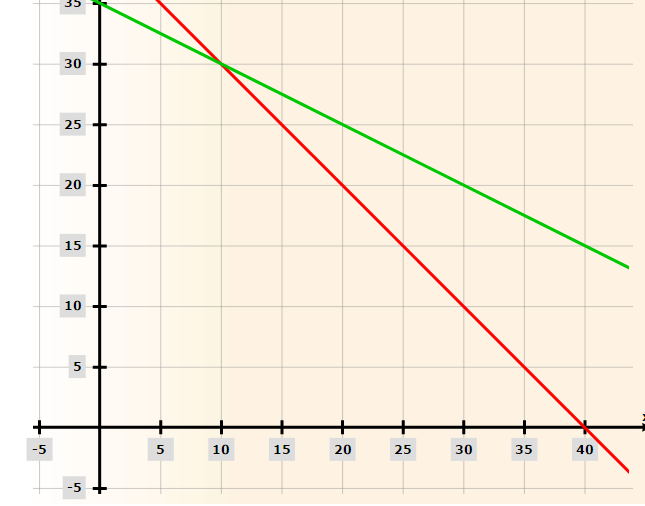
x + y = 40 acres (1) (for areas; x = the area for crop A; y = the area for crop B).
10x + 20y = 700 (2) for the seed cost
or
x + 2y = 70
We have the following system of equations:
x + y = 40
x + 2y = 70
The additional obvious restrictions are x >= 0 and y >= 0.
The graph is:
The objective function is the profit:
F(x, y) = 60x + 70y
According to the conception/ideology of the linear programming method, we need to evaluate the
objective function F(x, y) = 60x + 70y in three points (corner points):
(0, 40), (35, 0) and (10, 30)
We need to find the point where the objective function is maximal:
F(0, 40) = 60*0 + 70*40 = $2,800
F(35, 0) = 60*35 + 70*0 = $2,100
F(10, 30) = 60*10 + 70*30 = $2,700
Follows, the farmer should plant 40 acres of crop B.