Problema Solution
a rancher has 1200 feet of fencing to build adjacent rectangular corrals of equal lengths and widths. what is the maximum area that can be enclosed in the fencing? what are the dimensions on the corals?
Answer provided by our tutors
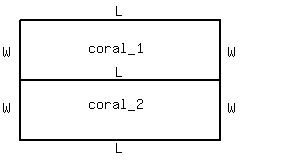
Let 'L' represent the length of each corral and 'W' the width of each corral.
We have the following equation 3L + 4W = 1200, from which we have W = (1200 - 3L)/4
The area of the two corals is:
A = L*2W
A = L*2*(1200 - 3L)/4
A = -(3/2)L^2 + 600L
We need to find L such that A had maximum:
L max = -b/2a, where a = -3/2, b = 600
L max = - 600/(2*(-3/2))
L max = 200 ft
W max = (1200 - 3*200)/4
W max = 150 ft
A max = 200*2*150
A max = 60,000 ft^2
The dimensions of each corral are 200 ft by 150 ft.
The maximum area enclosed in the two corrals is 60,000 ft^2.