Problema Solution
A square is inscribed in a circle and circumscribed about a smaller, concentric circle. What is the ratio of area of the inner circle to the area of the annulus (ring outside the inner circle and inside the outside circle)?
Answer provided by our tutors
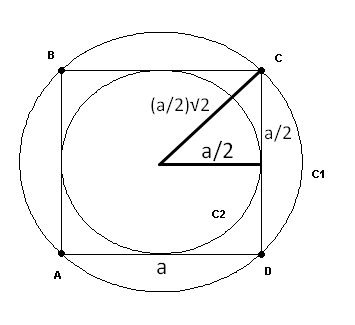
The area of the inner circle is:
C2 = ((a/2)^2)pi
C2 = (a^2)(pi/4)
The area of the outside circle is:
C1 = ((a/2)√2)^2 pi
C1 = (a^2)(pi/2)
The area of the annulus is:
C1 - C2 = (a^2)(pi/2 - pi/4)
C1 - C2 = (a^2)(pi/2)
The ratio of area of the inner circle to the area of the annulus is:
C2 : (C1 - C2) = (a^2)(pi/4) : (a^2)(pi/2) = (1/4) : (1/2) = 2/4 = 1/2