Problema Solution
A survey team is trying to estimate the height of a mountain above a level plain. From one point on the plain, they observe that the angle of elevation to the top of the mountain is 27 ^\circ. From a point 1000 feet closer to the mountain along the plain, they find that the angle of elevation is 31 ^\circ.
How high (in feet) is the mountain?
Answer provided by our tutors
Let
h = the height of the mountain
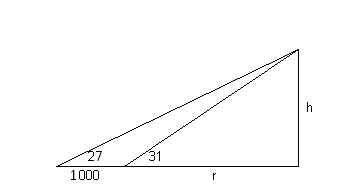
We will use the right triangle and the tangent function to find h:
tan 31 = h/r follows r = h/tan 31
tan 27 = h/(r + 1000)
Plug r = h/tan 31 into tan 27 = h/(r + 1000):
tan 27 = h/((h/(tan 31)) + 1000)
........
click here to see the equation solved for h
........
h = 3,351.98 ft
The mountain is 3,351.98 feet high.