Problema Solution
Among all pairs of numbers (x,y) such that 4x+2y=18, find the pair for which the sum of squares, x^2+y^2, is minimum. Write your answers as fractions reduced to lowest terms.
Answer provided by our tutors
First we will solve '4x+2y=18' for 'y'
Click here to see the step by step solving for y
........
y = -2x + 9
Plug the value y = -2x + 9 into 'x^2+y^2' and we need to find the minimum for the function:
f(x) = x^2 + (-2x + 9)^2
We can graph the above function to see the vertex.
Click here to see the graph for f(x) = x^2 + (-2x + 9)^2
Since the general functional notation f(x) is not supported we will replace it with variable 'z' and that it why we have the graph of:
z = x^2 + (-2x + 9)^2
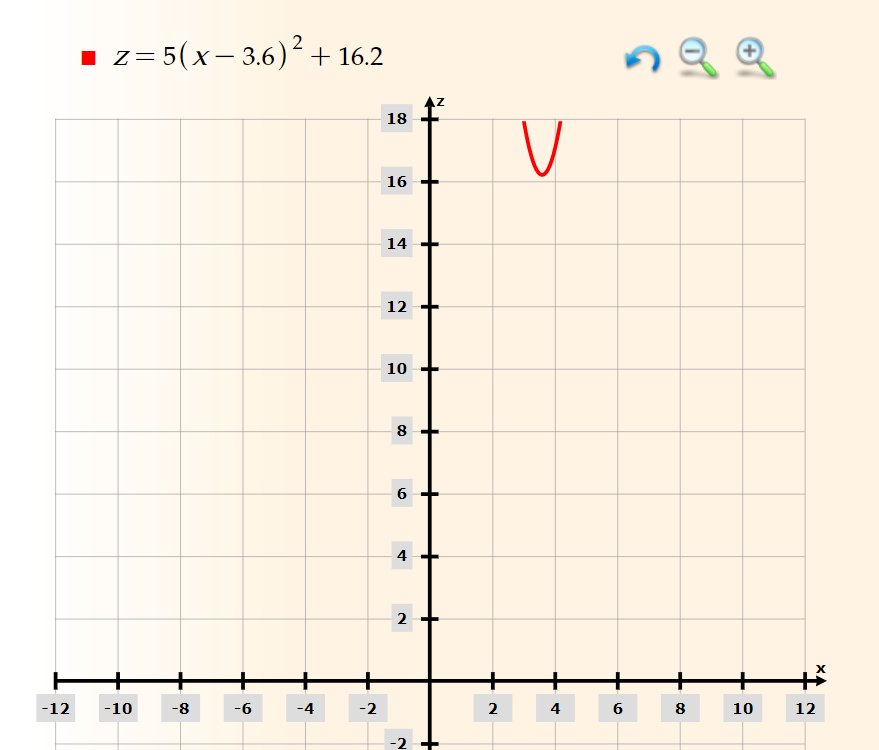
The minimum for the function is reached for the pair, the vertex of the graph, (3.6, 16.2).