Let 'x' and 'y' represent the dimensions of each of the three courts:

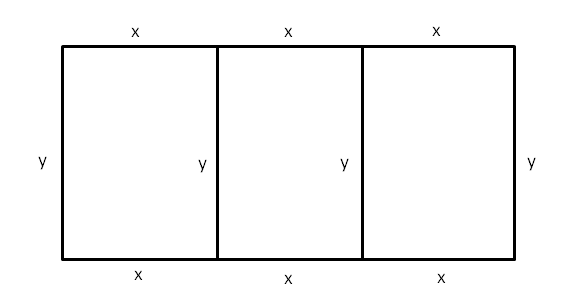
x and y are positive numbers.

940 feet of fencing is used to enclose the 3 courts:

6x + 4y = 940

........

click here to see the equation solved for y

........

y = (-3/2)x + 235

The total area of the 3 courts altogether is 19,800 ft^2:

3*xy = 19,800

Plug y = (-3/2)x + 235 into 3*xy = 19,800 and solve for x:

3x((-3/2)x + 235) = 19800

........

click here to see the equation solved for x

........

x1 = 120

x2 = 36.67

For x = 120 ft we have y = (-3/2)*120 + 235 = 55 ft.

For x = 36.67 ft we have  y = (-3/2)*36.67 + 235 = 180 ft.

One solutions for the dimensions, in feet, of the entire rectangular area is:

3x = 3*120 = 360 ft and 55 ft.

Second solution for the dimensions, in feet, of the entire rectangular area is:

3x = 3*36.67 = 110 ft and 180 ft.