Problema Solution
Heron's formula gives the area of a triangle that has sides of length a,b, and c. The formula is A= (square root) s(s-a)(s-b)(s-c), where s (called the semiperimeter) is defined by s=1/2(a+b+c).
A city council wants to build a nature preserve and sets aside a triangular piece of land whose sides are 555 yds, 448 yds and 635 yds. Use Heron's formula to find the area of the preserve.
Answer provided by our tutors
The following information is given:
a = 555 yd
b = 448 yd
c = 635 yd
Plug the values for a, b and c into s = (1/2)(a + b + c):
s = (1/2)(555 + 448 + 635)
s = 819
Next we use Heron's formula to find the area:
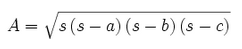
A = √(819(819 - 555)(819 - 448)(819 - 635))
A = √(1.4759769*10^10)
A = 121,489.79 yd^2
The area of to preserve is 121,489.79 yd^2.