The standard form equation of a circle with center at (h, k) and radius 'r' (r >=0) is:

(x - h)^2 + (y - k)^2 = r^2

First we will find (h, k) as the middle point of the segment with end points (−6, 6) and (6, −2):

h = (1/2)(6 + (-6))

h = 0

k = (1/2)(- 2 + 6)

k = 2

The center is (0, 2).

Next, we will find the radius:

r^2 = (0 - (-6))^2 + (2 - 6)^2

r^2 = 36 + 16

r^2 = 52

The standard for of equation is:

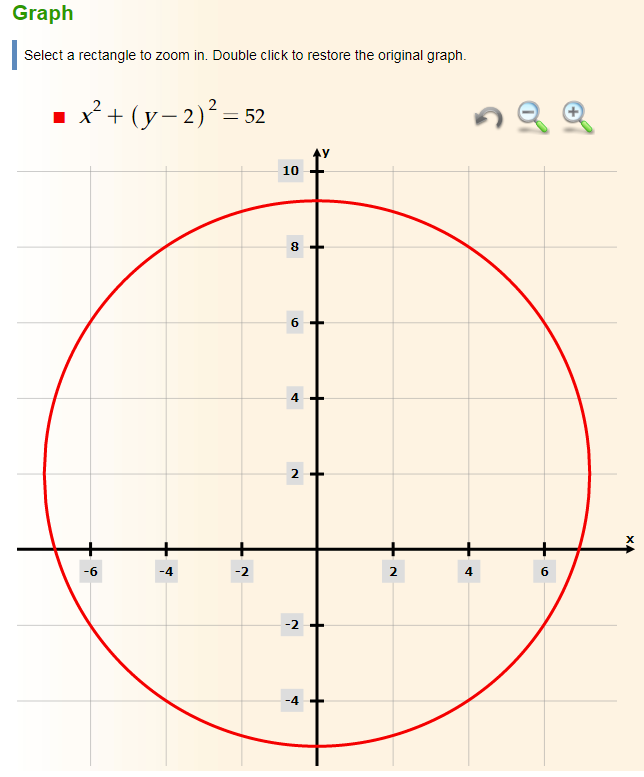
(x - 0)^2 + (y - 2)^2 = 52

x^2 + (y - 2)^2 = 52

click here to see the graph