Problema Solution
lunch stand makes $.75 in profit on each chef’s salad and $1.20 in profit on each Caesar salad. On a typical weekday, it sells between 40 and 60 chef’s salads and between 35 and 50 Caesar salads. The total number sold has never exceeded 100 salads. How many of each type of salad should be prepared to maximize profit?
Answer provided by our tutors
Let
x = the number of chef salads, x>=0
y = the number of Caesar salads, y>=0
The constrains are:
40 <= x <= 60
35 <= y <= 50
x + y <= 100
The objective function is F(x, y) = 0.75x + 1.20y
To find the maximum of the of objective function first we need to find the corner points of the above system of inequalities (the constrains):
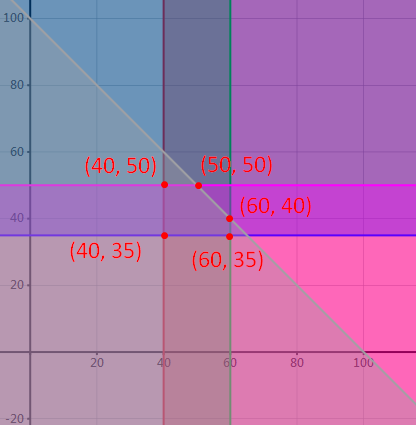
The corner points are (40, 35), (60, 35), (60, 40), (50, 50) and (40, 50).
F(40, 35) = 0.75*40 + 1.20*35 = $72
F(60, 35) = 0.70*60 + 1.20*35 = $84
F(60, 40) = 0.75*60 + 1.20*40 = $93
F(50, 50) = 0.75*50 + 1.20*50 = $97.50
F(40, 50) = 0.75*40 + 1.20*50 = $90
We conclude to maximize the profit 50 Chef and 50 Caesar salads should be prepared.