Since the order of the selected players is not of importance we will use combinations to solve. 

The number of p-combinations from a set of n elements is:

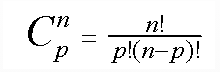
In our case p = 3 and n = 4

We need to find the number of 3-combinations from a set of 4 elements:

C(4,3) = 4!/(3!(4-3)!)

C(4, 3) = 4!/(3!1!)

C(4, 3) = 4

There are 4 different committees of 3 members that could be possibly formed.

You can also denote the members as A, B, C and D and write down all the possible committees and that would be all the possible subsets of 3 elements of the set {A, B, C, D}:

{A, B, C}

{A, B, D}

{A, C, D}

{B, C, D}