Assuming the given points of the streight line are (8, 638), (12, 552) and (18, 828) the slope can be calculted by the formula:

slope =(y₂ - y₁)/(x₂ - x₁), where (x₁, y₁) and (x₂, y₂) are the coordinates of two points on the line

So for (x1, y1) = (6, 638) amd (x2, y2) = (12, 552) we get

slope = (552 - 638)/(12 - 6)

slope = - 43/3

For (x1, y1) = (18, 828) amd (x2, y2) = (12, 552) we get

slope = (552 - 828)/(12 - 18)

slope = 46

We got 2 different values for the slope, meaning the 3 above points so the graph is not a streight line.

There is information missing in the question, is the line drawn trought the points prabolic?

If the graph is parabola then the equation is:

y = ax^2 + bx + c

and the slope is calculated using the formula:

slope = 2ax + b

By plugging the given points we get the system of equations:

638 = 64a + 8b + c

552 = 144a + 12b + c

688 = 324a + 18b + c

By solving the above system you can find the values for "a", "b" and "c":

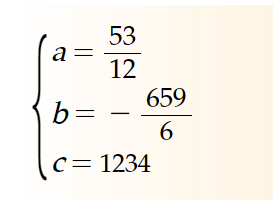
And then calculate the slope.