Problema Solution
The amount of revenue a company makes per day by selling x items is given by the function f(x) = 14 x – 0.2x2 . How many items should be sold if the company wants to maximize their profit?
Answer provided by our tutors
The function f(x) = 14x - 0.2x^2 has maximum since the quotient in front of x^2 is negative (-0.2 < 0).
We can also see that from graph of the function y = 14x - 0.2x^2
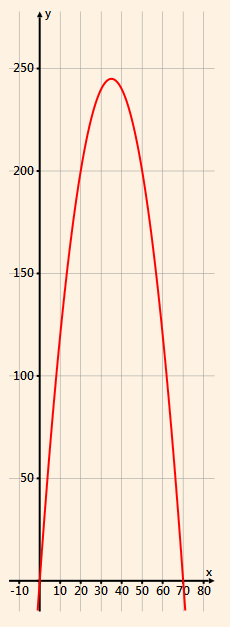
The function has maximum in:
x max = -b/2a, where a = -0.2, b = 14
x max = -14/(2*(-0.2))
x max = 35
The company should sell 35 items to maximize the profit.